题目内容
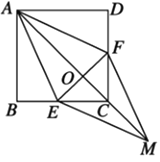
【题目】如图,在正方形ABCD中,AB=4,AC与![]() 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交
相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交![]() 于点N′,则PN-MN′的值为( )
于点N′,则PN-MN′的值为( )
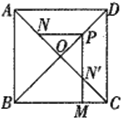
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据正方形的性质可得点O为AC的中点,根据三角形中位线的性质可求出PN的长,由PM⊥BC可得PM//CD,根据点P为OD中点可得点N′为OC中点,即可得出AC=4CN′,根据MN′//AB可得△CMN′∽△CBA,根据相似三角形的性质可求出MN′的长,进而可求出PN-MN′的长.
∵四边形ABCD是正方形,AB=4,
∴OA=OC,AD=AB=4,
∵N是AO的中点,P是OD的中点,
∴PN是△AOD的中位线,
∴PN=![]() AD=2,
AD=2,
∵PM⊥BC,
∴PM//CD//AB,
∴点N′为OC的中点,
∴AC=4CN′,
∵PM//AB,
∴△CMN′∽△CBA,
∴![]()
![]() ,
,
∴MN′=1,
∴PN-MN′=2-1=1,
故选:A.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目