Question

【题目】如图，中，，，，将绕顶点逆时针旋转到处，此时线段与的交点恰好为的中点，则的面积为______.

Answer 1

【答案】

【解析】

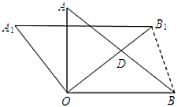
A1B1与OA相交于点E，作B1H⊥OB于点H，如图，利用勾股定理得到AB=10，再根据直角三角形斜边上的中线性质得OD=AD=DB，则∠1=∠A，接着根据旋转的性质得∠3=∠2，A1B1=AB=10，OB1=OB=8，OA1=OA=6，易得∠2+∠1=90°，所以∠OEB1=90°，于是可利用面积法计算出OE，再由四边形OEB1H为矩形得到B1H=OE，根据三角形的面积公式即可得出结论．

A1B1与OA相交于点E，作B1H⊥OB于点H，如图，

∵∠AOB=90°，AO=6，BO=8，

∴AB10．

∵D为AB的中点，

∴OD=AD=DB，

∴∠1=∠A．

∵△AOB绕顶点O逆时针旋转得到△A1OB1，

∴∠3=∠2，A1B1=AB=10，OB1=OB=8，OA1=OA=6．

∵∠3+∠A=90°，

∴∠2+∠1=90°，

∴∠OEB1=90°．

∵OEA1B1OB1OA1，

∴OE．

∵∠B1EO=∠EOB=∠OHB1=90°，

∴四边形OEB1H为矩形，

∴B1H=OE，

∴的面积===．

故答案为：．