题目内容
16.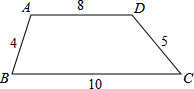 在四边形ABCD中,AD∥BC,AB与CD不平行,根据图中数据,若BA、CD延长后交于点M,则△MBC的周长为55.
在四边形ABCD中,AD∥BC,AB与CD不平行,根据图中数据,若BA、CD延长后交于点M,则△MBC的周长为55.
分析 由AD∥BC,得到△ADM∽△BCM,根据对应线段成比例列出方程$\frac{MA}{MB}$=$\frac{MD}{MC}$=$\frac{AD}{BC}$=$\frac{8}{10}$=$\frac{4}{5}$,解出MB=20,MC=25,由三角形的周长公式求出答案.
解答 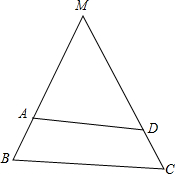 解:如图,∵AD∥BC,
解:如图,∵AD∥BC,
∴△ADM∽△BCM,
∴$\frac{MA}{MB}$=$\frac{MD}{MC}$=$\frac{AD}{BC}$=$\frac{8}{10}$=$\frac{4}{5}$,
∴AM=16,MD=20,
∴MB=20,MC=25,
∴△MBC的周长=20+10+25=55.
故答案为:55.
点评 本题考查了相似三角形的判定和性质,三角形的周长的求法,正确的找准对应线段是解题的关键.

练习册系列答案
相关题目
11.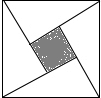 由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
 由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )| A. | 1 | B. | 3 | C. | 4-2$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
8. 已知某几何体的三视图如图所示,则该几何体是( )
已知某几何体的三视图如图所示,则该几何体是( )
 已知某几何体的三视图如图所示,则该几何体是( )
已知某几何体的三视图如图所示,则该几何体是( )| A. | 圆柱 | B. | 棱柱 | C. | 圆锥 | D. | 三棱锥 |
5.下列计算正确的是( )
| A. | 2a-a=1 | B. | a2+a2=2a4 | C. | a2•a3=a5 | D. | (a-b)2=a2-b2 |
6. 如图所示的工件的俯视图是( )
如图所示的工件的俯视图是( )
 如图所示的工件的俯视图是( )
如图所示的工件的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
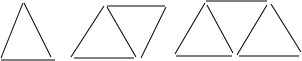 用牙签按下图的方式搭三角形,搭n个这样的三角形需要2n+1根牙签.
用牙签按下图的方式搭三角形,搭n个这样的三角形需要2n+1根牙签.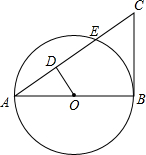 如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.
如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.