题目内容
13.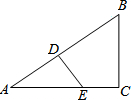 如图,在△ABC中,∠C=90°,点D在AB上,BC=BD,DE⊥AB交AC于点E.△ABC的周长为12,△ADE的周长为6.则BC的长为3.
如图,在△ABC中,∠C=90°,点D在AB上,BC=BD,DE⊥AB交AC于点E.△ABC的周长为12,△ADE的周长为6.则BC的长为3.
分析 设BC=BD=x,AD=y,△ABD和△ABC相似,根据相似三角形的性质:相似三角形周长的比等于对应边的比进行解答.
解答 解:设BC=BD=x,AD=y,
因为∠C=∠ADE=90°∠A=∠A,
所以△ADE∽△ACB;
两三角形的周长之比为1:2,
所以AD:AC=1:2,
则AC=2y;
根据三角形ABC的周长为12得:x+(x+y)+2y=12;即:2x+3y=12…①
根据勾股定理得:(2y)2+x2=(x+y)2,即:2x=3y…②
联合①②得:x=3,y=2;
∴BC=3.
故答案为:3.
点评 本题考查了相似三角形的性质和勾股定理的应用.首先根据△ADE和△ACB有两个角相等判定△ADE∽△ACB,然后根据相似三角形的性质:相似三角形周长的比等于对应边长的比得出AC的长度,然后利用勾股定理结合周长的计算公式算出BC的值.

练习册系列答案
相关题目
8.下列各组的三条线段中,不能组成三角形的是( )
| A. | 2,2,1 | B. | 5,2,4 | C. | 1,1,2 | D. | 5,6,7 |

 如图所示,AB=DC,AC=DB.
如图所示,AB=DC,AC=DB.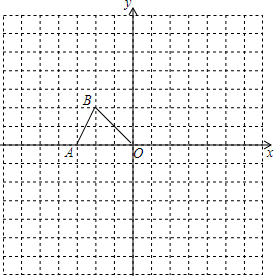 如图,在平面直角坐标系中,△AOB的位置如图所示,图中小正方形的边长均为1,请画出△AOB以点O为位似中心,放大到原来的2倍的位似图形,并写出放大后三角形三个顶点的坐标.
如图,在平面直角坐标系中,△AOB的位置如图所示,图中小正方形的边长均为1,请画出△AOB以点O为位似中心,放大到原来的2倍的位似图形,并写出放大后三角形三个顶点的坐标.