题目内容
如图都是由若干圆圈组成的正方形图案，正方形每条边（包括两个顶点）上都有n（n≥2）个圆圈，每个图案中圆圈的总个数为S，试写出S与n之间的函数表达式，并指出自变量n的取值范围，S能等于2014吗？为什么？
考点：函数关系式,规律型：图形的变化类
专题：
分析：根据观察，可得规律，根据规律，可得函数关系式．
解答：解；S与n之间的函数表达式S=n2（n≥2）；
S不能等于2014，理由如下：
当S=2014时，n=
＞
=48，
n不是正数，S不能等于2014．
S不能等于2014，理由如下：
当S=2014时，n=
| 2014 |
| 2004 |
n不是正数，S不能等于2014．
点评：本题考查了函数关系式，利用了图形蕴涵的规律：S=n2．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
如图，要使△CBD与△CAB相似，需加上什么条件？（请写出三个）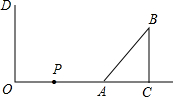
如图，在墙面OD（OD⊥OC）的右侧有一个Rt△ACB，∠ACB=90°，BC=3cm，AB=5cm，且OA=8cm，点P从点O出发，以1cm/s的速度在射线OA上运动，点Q在OD上运动，P、Q同时从O开始运动，设运动时间为t（s）．已知点A（-3，y1）、B（-1，y2）、C（2，y3）都在反比例函数y=
（k＜0）图象上，则正确的是（ ）
| k |
| x |
| A、y1＜y2＜y3 |
| B、y3＜y2＜y1 |
| C、y3＜y1＜y2 |
| D、y2＜y1＜y3 |