题目内容
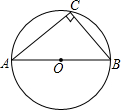 如图,△ABC内接于⊙O,AB为⊙O的直径,BC=6,AC=8.
如图,△ABC内接于⊙O,AB为⊙O的直径,BC=6,AC=8.求:(1)cosA和sinA的值;
(2)sin∠BOC和tan∠BOC的值.
考点:圆周角定理,解直角三角形
专题:
分析:(1)AB为直径可知△ABC为直角三角形,且可求得AB=10,利用三角函数的定义可求得cosA和sinA;
(2)过C作CD⊥AB,交AB于点D,可求得CD的长和OD的长,进一步利用三角函数的定义可求得sin∠BOC和tan∠BOC的值.
(2)过C作CD⊥AB,交AB于点D,可求得CD的长和OD的长,进一步利用三角函数的定义可求得sin∠BOC和tan∠BOC的值.
解答:解:
(1)∵AB为⊙O的直径,
∴∠ACB=90°,且BC=6,AC=8,
∴AB=10,
∴cosA=
=
=
,sinA=
=
=
;
(2)连接OC,过C作CD⊥AB于点D,
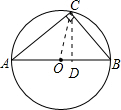
在Rt△ABC中,由面积相等可得:AB•CD=AC•BC,可求得CD=
=
=
,
在Rt△COD中,OC=
AB=5,由勾股定理可求得OD=
,
∴sin∠BOC=
=
=
,tan∠BOC=
=
=
.
(1)∵AB为⊙O的直径,
∴∠ACB=90°,且BC=6,AC=8,
∴AB=10,
∴cosA=
| AC |
| AB |
| 8 |
| 10 |
| 4 |
| 5 |
| BC |
| AB |
| 6 |
| 10 |
| 3 |
| 5 |
(2)连接OC,过C作CD⊥AB于点D,

在Rt△ABC中,由面积相等可得:AB•CD=AC•BC,可求得CD=
| AC•BC |
| AB |
| 6×8 |
| 10 |
| 24 |
| 5 |
在Rt△COD中,OC=
| 1 |
| 2 |
| 7 |
| 5 |
∴sin∠BOC=
| CD |
| CO |
| ||
| 5 |
| 24 |
| 25 |
| CD |
| OD |
| ||
|
| 24 |
| 7 |
点评:本题主要考查三角函数的定义及圆周角定理、勾股定理的应用,掌握三角函数的定义是解题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
已知点A(-3,y1)、B(-1,y2)、C(2,y3)都在反比例函数y=
(k<0)图象上,则正确的是( )
| k |
| x |
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y3<y1<y2 |
| D、y2<y1<y3 |
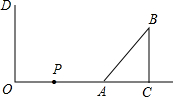 如图,在墙面OD(OD⊥OC)的右侧有一个Rt△ACB,∠ACB=90°,BC=3cm,AB=5cm,且OA=8cm,点P从点O出发,以1cm/s的速度在射线OA上运动,点Q在OD上运动,P、Q同时从O开始运动,设运动时间为t(s).
如图,在墙面OD(OD⊥OC)的右侧有一个Rt△ACB,∠ACB=90°,BC=3cm,AB=5cm,且OA=8cm,点P从点O出发,以1cm/s的速度在射线OA上运动,点Q在OD上运动,P、Q同时从O开始运动,设运动时间为t(s).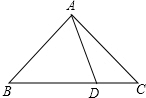 如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证:BD2+CD2=2AD2.
如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证:BD2+CD2=2AD2.