题目内容
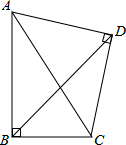 Rt△ABC中,∠ABC=90°,以AC为斜边作等腰直角△ADC,∠ADC=90°,AD=CD,求证:∠DBC=45°.
Rt△ABC中,∠ABC=90°,以AC为斜边作等腰直角△ADC,∠ADC=90°,AD=CD,求证:∠DBC=45°.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:作DE⊥BE,DF⊥AB,易证∠DAF=∠DCE,进而可证△ADF≌△CDE,可得DF=DE,根据角平分线性质即可解题.
解答:解:作DE⊥BE,DF⊥AB,
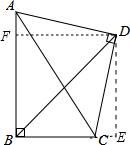
则∠AFD=∠CED,
∵四边形ABCD中,∠DAF+∠BCD+∠ABC+∠ADC=360°,
∠ADC=∠ABC=90°,
∴∠DAF+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DAF=∠DCE,
在△ADF和△CDE中,
,
∴△ADF≌△CDE(AAS),
∴DF=DE,
∴BD是∠ABC的角平分线,
∴∠DBC=45°.

则∠AFD=∠CED,
∵四边形ABCD中,∠DAF+∠BCD+∠ABC+∠ADC=360°,
∠ADC=∠ABC=90°,
∴∠DAF+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DAF=∠DCE,
在△ADF和△CDE中,
|
∴△ADF≌△CDE(AAS),
∴DF=DE,
∴BD是∠ABC的角平分线,
∴∠DBC=45°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中构建并求证△ADF≌△CDE是解题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
下列事件中是随机事件的是( )
| A、度量三角形的内角和,结果是360° |
| B、从装有5个黑球的口袋中摸出一球是黑球 |
| C、实数a的平方为负数 |
| D、购买100张中奖率为1%的彩票,结果中奖 |
 如图,在Rt△ABC中,∠C=90°,⊙O是Rt△ABC的内切圆,⊙O与AB相切于点D,且AD=1,BD=0.5,求△ABC的面积.
如图,在Rt△ABC中,∠C=90°,⊙O是Rt△ABC的内切圆,⊙O与AB相切于点D,且AD=1,BD=0.5,求△ABC的面积.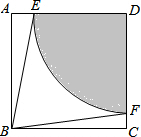 如图,以正方形ABCD的顶点D为圆心画圆,分别交AD,CD两边于点E,F.若∠ABE=15°,BE=4,则扇形DEF的面积是
如图,以正方形ABCD的顶点D为圆心画圆,分别交AD,CD两边于点E,F.若∠ABE=15°,BE=4,则扇形DEF的面积是