题目内容
已知线段AB=14,在AB上有四个点C,D,M,N,且AC:CD:DB=1:2:4,AM=
AC,DN=
DB,计算线段MN的长.
| 1 |
| 2 |
| 1 |
| 6 |
考点:两点间的距离
专题:
分析:根据题意画出图形,分别求得CM,CD,DN的值即可求得线段MN的长,即可解题.
解答:解:画出图形

∵AC:CD:DB=1:2:4,AC+CD+DB=14,
∴AC=2,CD=4,BD=8,
∵AM=
AC,∴CM=1,
∵DN=
DB,∴DN=
=
,
∴MN=CM+CD+DN=1+4+
=
.

∵AC:CD:DB=1:2:4,AC+CD+DB=14,
∴AC=2,CD=4,BD=8,
∵AM=
| 1 |
| 2 |
∵DN=
| 1 |
| 6 |
| 8 |
| 6 |
| 4 |
| 3 |
∴MN=CM+CD+DN=1+4+
| 4 |
| 3 |
| 19 |
| 3 |
点评:本题考查了线段长度的计算,分别求出CM,CD,DN的长是解题的关键.

练习册系列答案
相关题目
下列结论错误的是( )
| A、三边平方之比为1:2:3的三角形是直角三角形 |
| B、三条边长之比为3:4:5的三角形是直角三角形 |
| C、三个内角之比为3:4:5的三角形是直角三角形 |
| D、三个角度之比为1:1:2的三角形是直角三角形 |
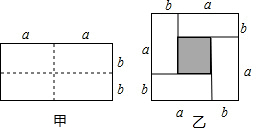 甲是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图乙形状拼成一个正方形.
甲是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图乙形状拼成一个正方形.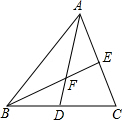 如图,点D、E是△ABC的边BC、AC的中点,分别连接AD、BE相交于点F,则BE:BF=
如图,点D、E是△ABC的边BC、AC的中点,分别连接AD、BE相交于点F,则BE:BF= Rt△ABC中,∠ABC=90°,以AC为斜边作等腰直角△ADC,∠ADC=90°,AD=CD,求证:∠DBC=45°.
Rt△ABC中,∠ABC=90°,以AC为斜边作等腰直角△ADC,∠ADC=90°,AD=CD,求证:∠DBC=45°. 如图是一个轴对称图形,AD所在的直线是对称轴,仔细观察图形,回答下列问题:
如图是一个轴对称图形,AD所在的直线是对称轴,仔细观察图形,回答下列问题: