题目内容
 如图,在Rt△ABC中,∠C=90°,⊙O是Rt△ABC的内切圆,⊙O与AB相切于点D,且AD=1,BD=0.5,求△ABC的面积.
如图,在Rt△ABC中,∠C=90°,⊙O是Rt△ABC的内切圆,⊙O与AB相切于点D,且AD=1,BD=0.5,求△ABC的面积.考点:三角形的内切圆与内心
专题:计算题
分析:作OE⊥BC于E,OF⊥AC于F,连结OD,如图,根据三角形内心的性质得点E、F为切点,则利用切线长定理得CE=CF,由⊙O与AB相切于点D,根据切线长定理得到AD=AF=1,BE=BD=
,设CE=x,则BC=x+
,AC=x+1,然后在Rt△ABC中利用勾股定理得(x+
)2+(x+1)2=(1+
)2,解得x1=
,x2=
(舍去),所以BC=
,AC=
,再根据三角形面积公式求解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
-3+
| ||
| 4 |
-3-
| ||
| 4 |
-1+
| ||
| 4 |
1+
| ||
| 4 |
解答:解:作OE⊥BC于E,OF⊥AC于F,连结OD,如图,
∵⊙O是Rt△ABC的内切圆,
∴点E、F为切点,
∴CE=CF,
∵⊙O与AB相切于点D
∴AD=AF=1,BE=BD=
,
设CE=x,则BC=x+
,AC=x+1,
在Rt△ABC中,∵BC2+AC2=AB2,
∴(x+
)2+(x+1)2=(1+
)2,解得x1=
,x2=
(舍去),
∴BC=
,AC=
,
∴△ABC的面积=
•
•
=
.

∵⊙O是Rt△ABC的内切圆,
∴点E、F为切点,
∴CE=CF,
∵⊙O与AB相切于点D
∴AD=AF=1,BE=BD=
| 1 |
| 2 |
设CE=x,则BC=x+
| 1 |
| 2 |
在Rt△ABC中,∵BC2+AC2=AB2,
∴(x+
| 1 |
| 2 |
| 1 |
| 2 |
-3+
| ||
| 4 |
-3-
| ||
| 4 |
∴BC=
-1+
| ||
| 4 |
1+
| ||
| 4 |
∴△ABC的面积=
| 1 |
| 2 |
-1+
| ||
| 4 |
1+
| ||
| 4 |
| 1 |
| 2 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了切线长定理.

练习册系列答案
相关题目
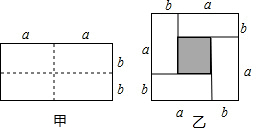 甲是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图乙形状拼成一个正方形.
甲是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图乙形状拼成一个正方形.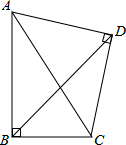 Rt△ABC中,∠ABC=90°,以AC为斜边作等腰直角△ADC,∠ADC=90°,AD=CD,求证:∠DBC=45°.
Rt△ABC中,∠ABC=90°,以AC为斜边作等腰直角△ADC,∠ADC=90°,AD=CD,求证:∠DBC=45°. 己知a,b,c在数轴上的位置如图,用“<”或“>”连接.
己知a,b,c在数轴上的位置如图,用“<”或“>”连接.