题目内容
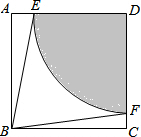 如图,以正方形ABCD的顶点D为圆心画圆,分别交AD,CD两边于点E,F.若∠ABE=15°,BE=4,则扇形DEF的面积是
如图,以正方形ABCD的顶点D为圆心画圆,分别交AD,CD两边于点E,F.若∠ABE=15°,BE=4,则扇形DEF的面积是考点:扇形面积的计算,正方形的性质
专题:
分析:连接EF,由条件可证明△ABE≌△CBF,可求得∠EBF=60°,且BE=BF,则△BEF为等边三角形,可求得EF,在Rt△DEF中,由勾股定理可求得DE的长,再利用扇形的面积公式计算即可.
解答: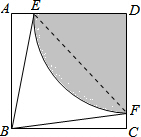 解:连接EF,
解:连接EF,
∵四边形ABCD为正方形,
∴AB=AC=DA=DC,∠A=∠C=∠D=∠ABC=90°,
∵DE=DF,
∴AE=CF,
在△ABE和△CBF中
∴△ABE≌△CBF(SAS),
∴BE=BF,∠ABE=∠CBF=15°,
∴∠EBF=90°-15°-15°=60°,
∴△BEF为等边三角形,
∴EF=BE=4,
在Rt△DEF中,DE=DF,且EF=4,
∴DE=2
,
∴S扇形DEF
=2π.
 解:连接EF,
解:连接EF,∵四边形ABCD为正方形,
∴AB=AC=DA=DC,∠A=∠C=∠D=∠ABC=90°,
∵DE=DF,
∴AE=CF,
在△ABE和△CBF中
|
∴△ABE≌△CBF(SAS),
∴BE=BF,∠ABE=∠CBF=15°,
∴∠EBF=90°-15°-15°=60°,
∴△BEF为等边三角形,
∴EF=BE=4,
在Rt△DEF中,DE=DF,且EF=4,
∴DE=2
| 2 |
∴S扇形DEF
| 90π•DE2 |
| 360 |
点评:本题主要考查扇形的计算及正方形的性质、等边三角形的判定和性质,证明△BEF为等边三角形求得EF的长是解题的关键.

练习册系列答案
相关题目
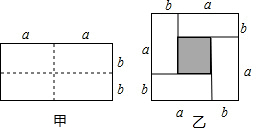 甲是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图乙形状拼成一个正方形.
甲是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图乙形状拼成一个正方形.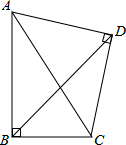 Rt△ABC中,∠ABC=90°,以AC为斜边作等腰直角△ADC,∠ADC=90°,AD=CD,求证:∠DBC=45°.
Rt△ABC中,∠ABC=90°,以AC为斜边作等腰直角△ADC,∠ADC=90°,AD=CD,求证:∠DBC=45°. 己知a,b,c在数轴上的位置如图,用“<”或“>”连接.
己知a,b,c在数轴上的位置如图,用“<”或“>”连接. 如图是一个轴对称图形,AD所在的直线是对称轴,仔细观察图形,回答下列问题:
如图是一个轴对称图形,AD所在的直线是对称轴,仔细观察图形,回答下列问题: