题目内容
10.已知两个连续正奇数的积是15,则这两个数中较小的一个数是3.分析 此题关键是熟悉连续的两个正奇数的差为2,可设这两个数为2n+1和2n+3,根据题意列方程求解即可.
解答 解:设这两个数为2n+1和2n+3,
由题意得:(2n+1)(2n+3)=15,
解得n=1或n=-3,
因为是连续的两个正奇数,所以n=-3舍去.
故答案为3.
点评 本题考查了一元二次方程的应用,关键是正确设出奇数,奇数的表示方法一般是2n-1或2n+1,根据题意列方程即可.

练习册系列答案
相关题目
15.如果|a|=-a,则a的值不可能等于( )
| A. | 3 | B. | -3 | C. | 0 | D. | (-7)7 |
2.下列判断中,错误的是( )
| A. | $\frac{π}{2}$不是分数,$\frac{π}{2}$是无理数 | |
| B. | 无理数包括正无理数、0和负无理数 | |
| C. | (1-x)2的平方根是x-1和1-x | |
| D. | 数轴上的点和所有的实数是一一对应的 |
20. 如图,在一幅长80cm,宽50cm的矩形树叶画四周镶一条金色的纸边,制成一幅矩形挂图,若要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,则满足的方程是( )
如图,在一幅长80cm,宽50cm的矩形树叶画四周镶一条金色的纸边,制成一幅矩形挂图,若要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,则满足的方程是( )
 如图,在一幅长80cm,宽50cm的矩形树叶画四周镶一条金色的纸边,制成一幅矩形挂图,若要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,则满足的方程是( )
如图,在一幅长80cm,宽50cm的矩形树叶画四周镶一条金色的纸边,制成一幅矩形挂图,若要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,则满足的方程是( )| A. | (80+x)(50+x)=5400 | B. | (80+2x)(50+2x)=5400 | C. | (80+2x)(50+x)=5400 | D. | (80+x)(50+2x)=5400 |
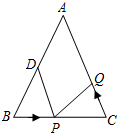 如图,已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
如图,已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动. 如图,将正方形OABC放在平面直角坐标系中,点A的坐标为(1,2),则点B的坐标是(-1,3).
如图,将正方形OABC放在平面直角坐标系中,点A的坐标为(1,2),则点B的坐标是(-1,3). 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=2cm,则线段BC=6cm.
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=2cm,则线段BC=6cm. 如图所示,在△ABC中:
如图所示,在△ABC中: