题目内容
1.某市救灾物资储备仓库共存储了A,B,C三类救灾物资,下面的统计图是三类物资存储量的不完整统计图.(1)求A类物资的存储量,并将两个统计表补充完整;
(2)现计划租用甲、乙两种货车共8辆,一次性将A、B两类物资全部运往某灾区.已知甲种货车最多可装A类物资10吨和B类物资40吨,乙种货车最多可装A、B类物资各20吨,则物资储备仓库安排甲、乙两种货车有几种方案?请你帮助设计出来.

分析 (1)根据扇形统计图可以得到A所占的比例,由C所占的比例和吨数可以求得ABC三种物资的存储总量,从而可以将扇形统计图和条形统计图补充完整;
(2)根据(1)可得到A、B两种物资的存储量,然后根据题意可以得到相应的不等式组,从而可以得到相应的设计方案.
解答 解:(1)根据扇形统计图的特点可知A所占的比例为:1-50%-37.5%=12.5%,
∵物资总量为:320÷50%=640吨,
∴A类物资的存储量为:640×12.5%=80吨,
∴补全的条形统计图和扇形统计图如下所示:
(2)由(1)可知,该存储库有A类物资80吨,B类物资240吨,
设将A、B两类物资全部运出需租用甲种货车x辆,
则$\left\{\begin{array}{l}{10x+20(8-x)≥80}\\{40x+20(8-x)≥240}\end{array}\right.$
解得4≤x≤8,
则x=4,5,6,7,8,
所以存储仓库有5种运输方案可以安排,
设计方案分别为:①甲车4辆,乙车4辆;
②甲车5辆,乙车3辆;
③甲车6辆,乙车2辆;
④甲车7辆,乙车1辆;
⑤甲车8辆,乙车0辆.
点评 本题考查一元一次不等式组的应用、扇形统计图、条形统计图,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
11.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | 2a3•3a2=6a6 | C. | (-2x3)4=8x12 | D. | (m-n)6÷(n-m)3=(n-m)3 |
6.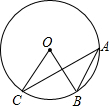 如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
 如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{2}$ |
10.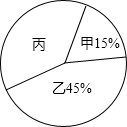 某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )
某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )
 某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )
某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )| A. | 80 | B. | 144 | C. | 200 | D. | 90 |
11.下列计算正确的是( )
| A. | x2+x3=x5 | B. | x2•x3=x6 | C. | x6÷x3=x3 | D. | (x3)2=x9 |
 如图,E是正方形ABCD的边BC的延长线上的一点,连接AE交DC于点F 若BC=4,CE=5,求CF的长.
如图,E是正方形ABCD的边BC的延长线上的一点,连接AE交DC于点F 若BC=4,CE=5,求CF的长.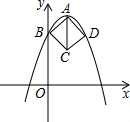 如图,在平面直角坐标系中,正方形ABCD的三个顶点A、B、D均在抛物线y=ax2-4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则AC长为4.
如图,在平面直角坐标系中,正方形ABCD的三个顶点A、B、D均在抛物线y=ax2-4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则AC长为4.