题目内容
将四个长为m，宽为n的长方形拼成如图的正方形，则图中阴影部分的面积可以用两种不同的方法表示，请通过观察写出（m-n）2，（m+n）2，mn之间的等量关系考点：完全平方公式的几何背景
专题：数形结合
分析：观察图形得到阴影部分为边长为m-n的正方形，则阴影部分的面积=（m-n）2，同时阴影部分的面积可以用边长为m+n的正方形的面积减去4个矩形的面积，即阴影部分的面积=（m+n）2-4mn，于是得到（m-n）2=（m+n）2-4mn．
解答：解：
阴影部分为边长为m-n的正方形，则阴影部分的面积=（m-n）2，
又因为阴影部分的面积=（m+n）2-4mn，
所以（m-n）2=（m+n）2-4mn．
故答案为（m-n）2=（m+n）2-4mn．
阴影部分为边长为m-n的正方形，则阴影部分的面积=（m-n）2，又因为阴影部分的面积=（m+n）2-4mn，
所以（m-n）2=（m+n）2-4mn．
故答案为（m-n）2=（m+n）2-4mn．
点评：本题考查了完全平方公式的几何背景：运用几何直观理解、解决完全平方公式的推导过程，通过几何图形之间的数量关系对完全平方公式做出几何解释．
练习册系列答案
相关题目
如图，点E是正方形内一点，△EDC是等边三角形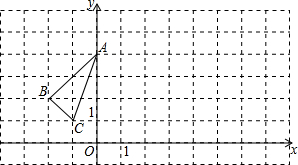
如图，已知在平面直角坐标系中，△ABC的位置如图．
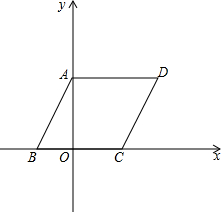如图，在平面直角坐标系中，四边形ABCD是平行四边形，AD=6，若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根，且OA＞OB．