题目内容
1. 如图,公里MN和小路PQ在点P处交汇,小路PQ上有一所学校A到公路MN的距离为80m,假如拖拉机行驶时,周围100m内受噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校A是否受到噪声影响?如果学校A受到影响,已知拖拉机速度为18km/h,那么学校A受到影响的时间为多长?
如图,公里MN和小路PQ在点P处交汇,小路PQ上有一所学校A到公路MN的距离为80m,假如拖拉机行驶时,周围100m内受噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校A是否受到噪声影响?如果学校A受到影响,已知拖拉机速度为18km/h,那么学校A受到影响的时间为多长?
分析 (1)由A点向MN作垂线AB,垂足为B,通过比较AB的长与100的大小,从而判断是否会受影响;
(2)利用勾股定理求得距离A点100米到离开100米的距离,除以拖拉机的速度即为影响学校的时间.
解答 解:(1)∵80<100,
∴学校会受到拖拉机的影响;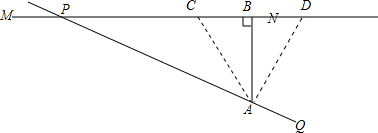
(2)假设当拖拉机行驶到C点开始影响学校,行驶到D点结束对学校的影响,
则AC=AD=100米,
∴BC=BD=$\sqrt{10{0}^{2}-8{0}^{2}}$=60米,
∴CD=2×60=120米,
∵18千米/时=5米/秒
所以影响学校的时间为:120÷5=24秒
∴拖拉机会影响学校,影响时间为24秒.
点评 本题考查了勾股定理的应用,解题时结合生活实际,准确理解题意是解决问题的关键.

练习册系列答案
相关题目
11.若a2+2ka+9是一个完全平方公式的展开式,则k等于( )
| A. | 3 | B. | ±6 | C. | -6 | D. | ±3 |
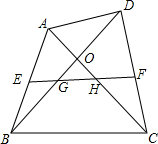 如图,在四边形ABCD中,AC与BD交于点O,E为AB中点,F为CD中点,EF分别与BD、AC交于点G、H.
如图,在四边形ABCD中,AC与BD交于点O,E为AB中点,F为CD中点,EF分别与BD、AC交于点G、H.