题目内容
11.若a2+2ka+9是一个完全平方公式的展开式,则k等于( )| A. | 3 | B. | ±6 | C. | -6 | D. | ±3 |
分析 先根据平方项确定出这两个数是a和3,再根据完全平方公式:(a±b)2=a2±2ab+b2的乘积二倍项列式求解即可.
解答 解:∵a2+2ka+9是一个完全平方式,
∴这两个数是a和3,
∴2ka=±2×3•a,
解得k=±3,
故选:D.
点评 本题是完全平方公式的应用,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.此题解题的关键是利用平方项求出这两个数.

练习册系列答案
相关题目
2.若点M的坐标为(x,y),且满足xy<0,则点M所在的象限为( )
| A. | 第一象限或第二象限 | B. | 第三象限或第四象限 | ||
| C. | 第一象限或第三象限 | D. | 以上答案都不对 |
3.已知△DEF≌△ABC,AB=AC,且△ABC的周长是23cm,BC=4cm,则△DEF的边长中必有一边等于( )
| A. | 9.5cm | B. | 9.5cm或9cm | C. | 4cm或9.5cm | D. | 9cm |
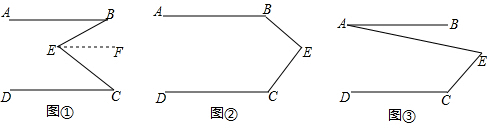
 已知:如图,AB=AC,DB=DC,点E在AD上,求证:EB=EC.
已知:如图,AB=AC,DB=DC,点E在AD上,求证:EB=EC.
 如图,公里MN和小路PQ在点P处交汇,小路PQ上有一所学校A到公路MN的距离为80m,假如拖拉机行驶时,周围100m内受噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校A是否受到噪声影响?如果学校A受到影响,已知拖拉机速度为18km/h,那么学校A受到影响的时间为多长?
如图,公里MN和小路PQ在点P处交汇,小路PQ上有一所学校A到公路MN的距离为80m,假如拖拉机行驶时,周围100m内受噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校A是否受到噪声影响?如果学校A受到影响,已知拖拉机速度为18km/h,那么学校A受到影响的时间为多长?