题目内容
 将正整数按如图所示的规律排列下去.若用有序数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示整数9,则(17,2)表示的数是
将正整数按如图所示的规律排列下去.若用有序数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示整数9,则(17,2)表示的数是考点:规律型:数字的变化类
专题:
分析:据(4,3)表示整数9,对图中给出的有序数对进行分析,可以发现:对所有数对(m,n)【n≤m】有:(m,n)=(1+2+3+…+m-1)+n=
+n.
| m(m-1) |
| 2 |
解答:解:若用有序数对(m,n)表示从上到下第m排,从左到右第n个数,
对如图中给出的有序数对和(4,3)表示整数9可得,
(4,3)=
+3=9;
(3,1)=
+1=4;
…,
由此可以发现,对所有数对(m,n)【n≤m】有:
(m,n)=(1+2+3+…+m-1)+n=
+n.
所以,(17,2)=
+2=136+2=138.
故答案为:138.
对如图中给出的有序数对和(4,3)表示整数9可得,
(4,3)=
| 4×(4-1) |
| 2 |
(3,1)=
| 3×(3-1) |
| 2 |
…,
由此可以发现,对所有数对(m,n)【n≤m】有:
(m,n)=(1+2+3+…+m-1)+n=
| m(m-1) |
| 2 |
所以,(17,2)=
| 17×(17-1) |
| 2 |
故答案为:138.
点评:此题考查对数字变化类知识点的理解和掌握,解答此类题目的关键是根据题目中给出的图形、数值、数列等已知条件,认真分析,找出规律,解决问题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
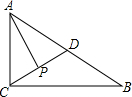 △ABC中,AC=3,BC=4,AB=5,D是AB中点,点P由C沿CD方向运动,每秒钟移1个单位,若△APD的面积为y,点P移动时间为x秒,
△ABC中,AC=3,BC=4,AB=5,D是AB中点,点P由C沿CD方向运动,每秒钟移1个单位,若△APD的面积为y,点P移动时间为x秒,