题目内容
若方程kx2-x+1=0没有实数根,则k的值为 .
考点:根的判别式
专题:
分析:根据已知条件“方程kx2-x+1=0没有实数根”可知该方程为一元二次方程k≠0,且根的判别式△=b2-4ac<0,据此可以列出关于k的不等式组,通过解不等式组可以求得k的取值范围.
解答:解:∵方程kx2-x+1=0没有实数根,
∴△=(-1)2-4k•1<0,即-4k+1<0,且k≠0,
解得k>
.
故答案是:k>
.
∴△=(-1)2-4k•1<0,即-4k+1<0,且k≠0,
解得k>
| 1 |
| 4 |
故答案是:k>
| 1 |
| 4 |
点评:本题考查了一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
同时考查了一元二次方程的定义.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
同时考查了一元二次方程的定义.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
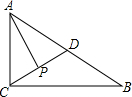 △ABC中,AC=3,BC=4,AB=5,D是AB中点,点P由C沿CD方向运动,每秒钟移1个单位,若△APD的面积为y,点P移动时间为x秒,
△ABC中,AC=3,BC=4,AB=5,D是AB中点,点P由C沿CD方向运动,每秒钟移1个单位,若△APD的面积为y,点P移动时间为x秒, 如图所示,△ABC中,AC⊥BC,BM平分∠ABC且交AC于点M,N是AB的中点且BN=BC.求证:
如图所示,△ABC中,AC⊥BC,BM平分∠ABC且交AC于点M,N是AB的中点且BN=BC.求证: