题目内容
 如图,已知圆锥的底面半径为9cm,PA=27cm,C为PB的中点,AB为底面直径,则在圆锥侧面上由点A到点C的最短路径是多少?
如图,已知圆锥的底面半径为9cm,PA=27cm,C为PB的中点,AB为底面直径,则在圆锥侧面上由点A到点C的最短路径是多少?考点:平面展开-最短路径问题
专题:
分析:最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.需先算出圆锥侧面展开图的扇形半径.看如何构成一个直角三角形,然后根据锐角三角函数的定义进行计算.
解答: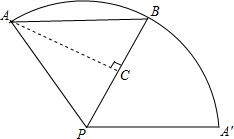 解:如图所示,
解:如图所示,
∴设圆心角为n,则
=2π×9,解得n=120°.
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90°.
∴AC=AP•sin60°=27×
=
.
 解:如图所示,
解:如图所示,∴设圆心角为n,则
| nπ×27 |
| 180 |
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90°.
∴AC=AP•sin60°=27×
| ||
| 2 |
27
| ||
| 2 |
点评:本题考查了圆锥的计算,需注意最短距离的问题最后都要转化为平面上两点间的距离的问题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下列语句中,不正确的是( )
| A、位似的图形都是相似的图形 |
| B、相似的图形都是位似的图形 |
| C、位似图形的位似比等于相似比 |
| D、位似中心可以在两个图形外部,也可以在两个图形内部 |
 如图:
如图: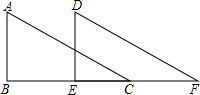 如图,Rt△ABC沿直角边BC所在直线向右平移得到△DEF,下列结论:
如图,Rt△ABC沿直角边BC所在直线向右平移得到△DEF,下列结论: 如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积是多少?
如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积是多少? 已知,如图,AD∥BC,∠1=∠2,∠3=∠E.试说明:AE∥CD.
已知,如图,AD∥BC,∠1=∠2,∠3=∠E.试说明:AE∥CD. 如图,在正方形铁皮上剪下一个扇形,又在剩余部分剪去一个最大的扇形.用它们能否围成一个圆锥?为什么?
如图,在正方形铁皮上剪下一个扇形,又在剩余部分剪去一个最大的扇形.用它们能否围成一个圆锥?为什么?