题目内容
11. 已知△ADE中,∠DAE=90°,AD=AE,点B为△ADE内一点,连接AB,将AB绕点A顺时针旋转90°到AC,连接BE、CD.
已知△ADE中,∠DAE=90°,AD=AE,点B为△ADE内一点,连接AB,将AB绕点A顺时针旋转90°到AC,连接BE、CD.(1)试说明△ABE≌△ACD;
(2)若BE=1,AB=2,BD=3,试求∠ACD的度数;
(3)在(2)的基础上,求四边形ABDC的面积(结果保留1位小数).
分析 (1)由旋转的性质得到∠AB=AC,∠CAB=∠DAE=90°,根据角的和差得到∠BAE=∠CAD,于是得到结论;
(2)连接BC,得到△ABC为等腰直角三角形,求得∠ACB=45°,BC=$\sqrt{2}$AB=2$\sqrt{2}$,根据全等三角形的性质得到CD=BE=1,根据勾股定理的逆定理得到∠BCD=90°,于是得到结论;
(3)四边形ABDC的面积=S△ABC+S△CBD,代入数据监控得到结论.
解答 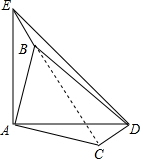 解:(1)∵将AB绕点A顺时针旋转90°到AC,
解:(1)∵将AB绕点A顺时针旋转90°到AC,
∴∠AB=AC,∠CAB=∠DAE=90°,
∴∠BAE=∠CAD,
在△ABE与△DAC中,$\left\{\begin{array}{l}{AE=AD}\\{∠BAE=∠CAE}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACD;
(2)连接BC,
∵BA=CA=2,∠BAC=90°,
∴△ABC为等腰直角三角形,
∴∠ACB=45°,BC=$\sqrt{2}$AB=2$\sqrt{2}$,
∵△ABE≌△ACD,
∴CD=BE=1,
∵BD=3,
∵BD2=BC2+CD2,
∴∠BCD=90°,
∴∠ACD=135°;
(3)四边形ABDC的面积=S△ABC+S△CBD=$\frac{1}{2}×$22+$\frac{1}{2}×$2$\sqrt{2}$×1=$\sqrt{2}$+2=3.4.
点评 本题考查了全等三角形的判定和性质,旋转的性质,等腰直角三角形的性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目

 如图,圆心角∠AOB=20°,将$\widehat{AB}$绕圆心旋转100°得到$\widehat{CD}$,则$\widehat{CD}$的度数是20°.
如图,圆心角∠AOB=20°,将$\widehat{AB}$绕圆心旋转100°得到$\widehat{CD}$,则$\widehat{CD}$的度数是20°. 如图,在△ABC中,AF=2BF,CE=3AE,CD=4BD.连接CF交DE于P点,求EP:DP的值.
如图,在△ABC中,AF=2BF,CE=3AE,CD=4BD.连接CF交DE于P点,求EP:DP的值.
 如图,在△ABC中,AE=EC,AD平分∠BAC,AD和CE是△ABC的高,且AD和CE相交于点H.
如图,在△ABC中,AE=EC,AD平分∠BAC,AD和CE是△ABC的高,且AD和CE相交于点H. 如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠A=56°,求∠EDF.
如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠A=56°,求∠EDF.