题目内容
6. 如图,在△ABC中,AF=2BF,CE=3AE,CD=4BD.连接CF交DE于P点,求EP:DP的值.
如图,在△ABC中,AF=2BF,CE=3AE,CD=4BD.连接CF交DE于P点,求EP:DP的值.
分析 连接EF、DF,根据共高两三角形的底边之比等于面积比可得$\frac{EP}{DP}$=$\frac{{S}_{△CPE}}{{S}_{△CPD}}$=$\frac{{S}_{△FPE}}{{S}_{△FPD}}$,由等比性质可得$\frac{EP}{DP}=\frac{{S}_{△CPE}+{S}_{△FPE}}{{S}_{△CPD}+{S}_{△FPD}}$=$\frac{{S}_{△CEF}}{{S}_{△CDF}}$,再根据AF=2BF、CE=3AE、CD=4BD知$\frac{CE}{AC}=\frac{3}{4}$、$\frac{CD}{BC}=\frac{4}{5}$、$\frac{AF}{AB}=\frac{2}{3}$、$\frac{BF}{AB}=\frac{1}{3}$,从而由$\frac{EP}{DP}$=$\frac{{S}_{△FPE}}{{S}_{△FPD}}$=$\frac{\frac{3}{4}{S}_{△ACF}}{\frac{4}{5}{S}_{△BCF}}$=$\frac{\frac{3}{4}×\frac{2}{3}{S}_{△ABC}}{\frac{4}{5}×\frac{1}{3}{S}_{△ABC}}$可得答案.
解答 解:如图,连接EF、DF,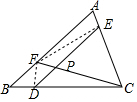
则$\frac{EP}{DP}$=$\frac{{S}_{△CPE}}{{S}_{△CPD}}$=$\frac{{S}_{△FPE}}{{S}_{△FPD}}$,
∵AF=2BF,CE=3AE,CD=4BD,
∴$\frac{CE}{AC}=\frac{3}{4}$,$\frac{CD}{BC}=\frac{4}{5}$,$\frac{AF}{AB}=\frac{2}{3}$,$\frac{BF}{AB}=\frac{1}{3}$,
∴$\frac{EP}{DP}=\frac{{S}_{△CPE}+{S}_{△FPE}}{{S}_{△CPD}+{S}_{△FPD}}$=$\frac{{S}_{△CEF}}{{S}_{△CDF}}$=$\frac{\frac{3}{4}{S}_{△ACF}}{\frac{4}{5}{S}_{△BCF}}$=$\frac{\frac{3}{4}×\frac{2}{3}{S}_{△ABC}}{\frac{4}{5}×\frac{1}{3}{S}_{△ABC}}$=$\frac{15}{8}$.
点评 本题主要考查比例线段的基本性质,根据共高两三角形的底边之比等于面积比将线段的比转化为面积的比是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | x=2 | B. | x=-2 | C. | x=1 | D. | x=1和-2 |
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跃情况 | +4 | -1 | +3.5 | -2.5 | -5 |
(1)星期三收盘时,该股票每股多少元?
(2)这周内该股收盘时的最高价、最低价分别是多少元?
(3)已知买入股票与卖出股票均需支付成交金额的千分之五的交易费,若小明的爸爸在周五以收盘价将全部股票卖出,他的收益情况如何?
 如图,已知三条直线AB、BC、CA两两相交,那么到这三条直线的距离都相等的点一共有4个.
如图,已知三条直线AB、BC、CA两两相交,那么到这三条直线的距离都相等的点一共有4个.
 已知△ADE中,∠DAE=90°,AD=AE,点B为△ADE内一点,连接AB,将AB绕点A顺时针旋转90°到AC,连接BE、CD.
已知△ADE中,∠DAE=90°,AD=AE,点B为△ADE内一点,连接AB,将AB绕点A顺时针旋转90°到AC,连接BE、CD. 如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.
如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.