题目内容
1．已知a、b、c为整数，a2+b2+c2+49-4a-6b-12c＜1，则（$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$）abc=1．分析 利用条件和因式分解可得：0≤（a-2）2+（b-3）2+（c-6）2＜1，即a=2，b=3，c=6，然后代入原式即可求出答案．
解答 解：∵a2+b2+c2+49-4a-6b-12c＜1，
∴（a-2）2+（b-3）2+（c-6）2＜1，
∵（a-2）2≥0，（b-3）2≥0，（c-6）2≥0，
∴0≤（a-2）2+（b-3）2+（c-6）2＜1，
∵a、b、c为整数，
∴（a-2）2+（b-3）2+（c-6）2也是整数，
∴（a-2）2+（b-3）2+（c-6）2=0，
∴a=2，b=3，c=6，
∴原式=（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{6}$）36=1
点评 本题考查分式化简求值，涉及因式分解，不等式的性质等知识，综合程度较高．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
相关题目
如图，直线y=x+t和抛物线y=x2+bx+c相交于A（1，0），B（4，3）两点，则t的值为-1，不等式x2+（b-1）x+c-t＞0的解集为x＜1或x＞4．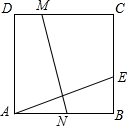
如图所示，四边形ABCD是边长为3的正方形，E是BC边上一点，且EC=2BE，将正方形折叠，使点A与点E重合，折痕为MN，若四边形BCMN的面积和四边形ADMN的面积分别为S1，S2．求S1：S2．
如图，已知方格纸中的小正方形边长为1，A，B，C均为网格纸上的格点，那么△ABC的面积为13．