题目内容
11．
如图，直线y=x+t和抛物线y=x2+bx+c相交于A（1，0），B（4，3）两点，则t的值为-1，不等式x2+（b-1）x+c-t＞0的解集为x＜1或x＞4．
分析 直接利用待定系数法求出t的值，进而利用函数图象得出答案．
解答 解：把A（1，0），代入y=x+t得：
0=1+t，
解得：t=-1，
不等式x2+（b-1）x+c-t＞0等价于x2+bx+c＞x+t，
由图象可得，当x＜1或x＞4，抛物线y=x2+bx+c的图象
位于直线y=x+t的上方，所以此时x2+bx+c＞x+t．
故答案为：-1；x＜1或x＞4．
点评 此题主要考查了二次函数与不等式，正确利用函数图象分析是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
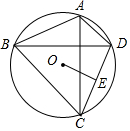如图，圆O中，弦AC⊥BD，且OE⊥CD于E，若AB的长是10，则OE的长是5．
如图：有一个圆柱，底面圆的直径AB=$\frac{16}{π}$，高BC=12，P为BC的中点，蚂蚁从A点爬到P点的最短距离是10．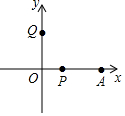
如图，在平面直角坐标系中有一点A，OA=16，动点P从A开始以每秒2个单位的速度向x轴负半轴运动，动点Q从0开始以每秒1个单位的速度向y轴正半轴运动，P，Q同时出发，设时间为t；