题目内容
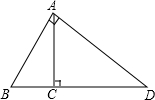 如图所示,∠BAD=90°,∠ACB=90°,∠ABD=60°,若AC=3,CD=
如图所示,∠BAD=90°,∠ACB=90°,∠ABD=60°,若AC=3,CD=考点:勾股定理,含30度角的直角三角形
专题:
分析:先根据∠BAD=90°,∠ACB=90°,∠ABD=60°得出∠BAC的度数,进而得出∠CAD的度数,根据直角三角形的性质即可得出结论.
解答:解:∵∠BAD=90°,∠ACB=90°,∠ABD=60°,
∴∠BAC=30°,
∴∠CAD=90°-30°=60°,
∴∠D=30°.
∵AC=3,
∴AD=2AC=6,
∴CD=
=
=3
.
故答案为:3
.
∴∠BAC=30°,
∴∠CAD=90°-30°=60°,
∴∠D=30°.
∵AC=3,
∴AD=2AC=6,
∴CD=
| AD2-AC2 |
| 62-32 |
| 3 |
故答案为:3
| 3 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
三角形三边长分别为8,15,17,则最短边上的高为( )
| A、8 | B、15 | C、16 | D、17 |
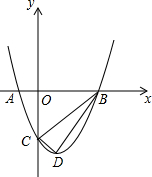 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D. 如图,△ABC被平行光照射,CD⊥AB于D,AB在投影面上,则AC的投影是什么?CD与BC的投影呢?
如图,△ABC被平行光照射,CD⊥AB于D,AB在投影面上,则AC的投影是什么?CD与BC的投影呢?