题目内容
一个三角形的两边长分别为1和2,第三边长为整数,则这个三角形的周长为 .
考点:三角形三边关系
专题:
分析:根据三角形的三边关系“第三边大于两边之差,而小于两边之和”,求得第三边的取值范围;再根据第三边是整数,从而求得周长.
解答:解:设第三边为x,
根据三角形的三边关系,得:2-1<x<2+1,
即1<x<3,
∵x为整数,
∴x的值为2.
三角形的周长为1+2+2=5.
故答案为:5.
根据三角形的三边关系,得:2-1<x<2+1,
即1<x<3,
∵x为整数,
∴x的值为2.
三角形的周长为1+2+2=5.
故答案为:5.
点评:此题考查了三角形的三边关系.关键是正确确定第三边的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
以下列选项中的数为长度的三条线段中,不能组成直角三角形的是( )
| A、8,15,17 |
| B、9,12,15 |
| C、4,6,8 |
| D、7,24,25 |
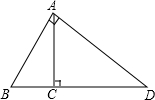 如图所示,∠BAD=90°,∠ACB=90°,∠ABD=60°,若AC=3,CD=
如图所示,∠BAD=90°,∠ACB=90°,∠ABD=60°,若AC=3,CD= 如图,在△ABC中,∠ACB=90°,∠B=40°,AE平分∠BAC,AC的垂直平分线DE分别与AC、AE交于点D、E,那么∠BCE=
如图,在△ABC中,∠ACB=90°,∠B=40°,AE平分∠BAC,AC的垂直平分线DE分别与AC、AE交于点D、E,那么∠BCE=