题目内容
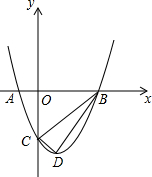 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.(1)求该抛物线的解析式与顶点D的坐标;
(2)P是线段BC上的一个动点,过P点作y轴的平行线交抛物线于点E,求线段PE长度的最大值是多少?
(3)探究坐标轴上是否存在点F,使得以F、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点F的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)利用待定系数法将A(-1,0)、B(3,0),C(0,-3),代入y=ax2+bx+c,求出二次函数解析式即可,然后利用配方法直接求出顶点坐标即可;
(2)首先求出BC的解析式,然后设出P点横坐标为m,表示出PE的长度,求出最大值;
(3)根据相似三角形的判定方法分别得出即可.
(2)首先求出BC的解析式,然后设出P点横坐标为m,表示出PE的长度,求出最大值;
(3)根据相似三角形的判定方法分别得出即可.
解答:解:(1)设该抛物线的解析式为y=ax2+bx+c,
由抛物线与y轴交于点C(0,-3),可知c=-3.
即抛物线的解析式为y=ax2+bx-3把A(-1,0)、B(3,0)代入,
得
,
解得
,
∴抛物线的解析式为y=x2-2x-3;
∵y=x2-2x-3=(x2-2x+1)-4,
=(x-1)2-4,
∴顶点D的坐标为(1,-4);
(2)∵B(3,0),C(0,-3),
∴BC的解析式为:y=x-3,
设P点横坐标为m,
则P点纵坐标为m-3,E点纵坐标为m2-2m-3,
PE=m-3-(m2-2m-3)=-m2+3m=-(m-
)2+
,
当m=
时,PE有最大值
;

(3)连接AC,
易得:CD=
,BC=3
,BD=2
,
则有CD2+CB2=BD2,
可知Rt△COA∽Rt△BCD,得符合条件的点为O(0,0)
过A作AF1⊥AC交y轴正半轴于F1,可知Rt△CAF1∽Rt△COA∽Rt△BCD,
求得符合条件的点为F1(0,
),
过C作CF2⊥AC交x轴正半轴于F2,可知Rt△F2CA∽Rt△COA∽Rt△BCD,
求得符合条件的点为F2(9,0).
综上所述:符合条件的点有三个:(0,0),F1(0,
),F2(9,0).
由抛物线与y轴交于点C(0,-3),可知c=-3.
即抛物线的解析式为y=ax2+bx-3把A(-1,0)、B(3,0)代入,
得
|
解得
|
∴抛物线的解析式为y=x2-2x-3;
∵y=x2-2x-3=(x2-2x+1)-4,
=(x-1)2-4,
∴顶点D的坐标为(1,-4);
(2)∵B(3,0),C(0,-3),
∴BC的解析式为:y=x-3,
设P点横坐标为m,
则P点纵坐标为m-3,E点纵坐标为m2-2m-3,
PE=m-3-(m2-2m-3)=-m2+3m=-(m-
| 3 |
| 2 |
| 9 |
| 4 |
当m=
| 3 |
| 2 |
| 9 |
| 4 |

(3)连接AC,
易得:CD=
| 2 |
| 2 |
| 5 |
则有CD2+CB2=BD2,
可知Rt△COA∽Rt△BCD,得符合条件的点为O(0,0)
过A作AF1⊥AC交y轴正半轴于F1,可知Rt△CAF1∽Rt△COA∽Rt△BCD,
求得符合条件的点为F1(0,
| 1 |
| 3 |
过C作CF2⊥AC交x轴正半轴于F2,可知Rt△F2CA∽Rt△COA∽Rt△BCD,
求得符合条件的点为F2(9,0).
综上所述:符合条件的点有三个:(0,0),F1(0,
| 1 |
| 3 |
点评:此题主要考查了二次函数的综合应用以及相似三角形的判定等知识,相似三角形与二次函数经常结合出综合题目,所以同学们学要对这些知识熟练地掌握才能正确的解答.

练习册系列答案
相关题目
以下列选项中的数为长度的三条线段中,不能组成直角三角形的是( )
| A、8,15,17 |
| B、9,12,15 |
| C、4,6,8 |
| D、7,24,25 |
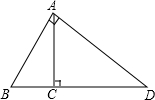 如图所示,∠BAD=90°,∠ACB=90°,∠ABD=60°,若AC=3,CD=
如图所示,∠BAD=90°,∠ACB=90°,∠ABD=60°,若AC=3,CD= 如图,在△ABC中,∠ACB=90°,∠B=40°,AE平分∠BAC,AC的垂直平分线DE分别与AC、AE交于点D、E,那么∠BCE=
如图,在△ABC中,∠ACB=90°,∠B=40°,AE平分∠BAC,AC的垂直平分线DE分别与AC、AE交于点D、E,那么∠BCE=