题目内容
6.已知:⊙O上两个定点A,B和两个动点C,D,AC与BD交于点E.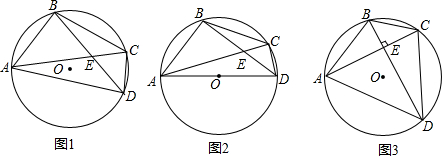
(1)如图1,求证:EA•EC=EB•ED;
(2)如图2,若$\widehat{AB}$=$\widehat{BC}$,AD是⊙O的直径,求证:AD•AC=2BD•BC;
(3)如图3,若AC⊥BD,点O到AD的距离为2,求BC的长.
分析 (1)根据同弧所对的圆周角相等得到角相等,从而证得三角形相似,于是得到结论;
(2)如图2,连接CD,OB交AC于点F由B是弧AC的中点得到∠BAC=∠ADB=∠ACB,且AF=CF=0.5AC.证得△CBF∽△ABD.即可得到结论;
(3)如图3,连接AO并延长交⊙O于F,连接DF得到AF为⊙O的直径于是得到∠ADF=90°,过O作OH⊥AD于H,根据三角形的中位线定理得到DF=2OH=4,通过△ABE∽△ADF,得到1=∠2,于是结论可得.
解答 (1)证明:∵∠EAD=∠EBC,∠BCE=∠ADE,
∴△AED∽△BEC,
∴$\frac{AE}{BE}=\frac{DE}{CE}$,
∴EA•EC=EB•ED;
(2)证明:如图2,连接CD,OB交AC于点F
∵B是弧AC的中点,
∴∠BAC=∠ADB=∠ACB,且AF=CF=0.5AC.
又∵AD为⊙O直径,
∴∠ABD=90°,又∠CFB=90°.
∴△CBF∽△DAB.
∴$\frac{CF}{BD}=\frac{BC}{AD}$,故CF•AD=BD•BC.
∴AC•AD=2BD•BC;
(3)解:如图3,连接AO并延长交⊙O于F,连接DF,
∴AF为⊙O的直径,
∴∠ADF=90°,
过O作OH⊥AD于H,
∴AH=DH,OH∥DF,
∵AO=OF,
∴DF=2OH=4,
∵AC⊥BD,
∴∠AEB=∠ADF=90°,
∵∠ABD=∠F,
∴△ABE∽△ADF,
∴∠1=∠2,
∴$\widehat{BC}=\widehat{DF}$,
∴BC=DF=4.
点评 本题考查了圆周角定理,垂径定理,相似三角形的判定和性质,三角形的中位线的性质,正确作出辅助线是解题的关键.

练习册系列答案
相关题目
1.在平面直角坐标系中,若直线y=kx+b经过第一、三、四象限,则直线y=bx+k不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.如图四个图形中,是中心对称图形的为( )
| A. |  | B. |  | C. |  | D. |  |
15.计算(-3x)2的结果是( )
| A. | 6x2 | B. | -6x2 | C. | 9x2 | D. | -9x2 |
 如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.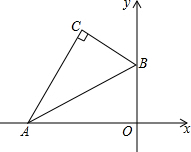 如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm
如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm 如图,在平面直角坐标系中,将点P(-4,2)绕原点顺时针旋转90°,则其对应点Q的坐标为(2,4).
如图,在平面直角坐标系中,将点P(-4,2)绕原点顺时针旋转90°,则其对应点Q的坐标为(2,4).