Question

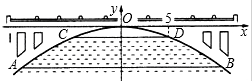如图，有一抛物线型拱桥，在正常水位使水面宽AB=20m，当水位上升3m，水面宽CD=10m．
（1）按如图所示的直角坐标系，求此抛物线的函数表达式；
（2）有一条船以5km/h的速度向此桥径直驶来，当船距离此桥35km，桥下水位正好在AB处，之后水位每小时上涨0.25m，当水位达到CD处时，将禁止船只通行，如果该船的速度不变，那么它能否安全通过此桥？

Answer 1

考点：二次函数的应用

专题：

分析：（1）以拱桥最顶端为原点，建立直角坐标系，根据题目中所给的数据设函数解析式为y=ax²，由待定系数法求出其解即可；
（2）计算出船行驶到桥下的时间，由这个时间按计算水位上升的高度，比较上升的高度与3的大小就可以求出结论．

解答：解：（1）设抛物线的解析式为y=ax²（a不等于0），桥拱最高点O到水面CD的距离为h米．
则D（5，-h），B（10，-h-3）
∴

25a=-h 100a=-h-3

，
解得

a=- 1 25 h=1

，
∴抛物线的解析式为y=-

1

25

x²；
（2）由题意，得
船行驶到桥下的时间为：35÷5=7小时，
水位上升的高度为：0.25×7=1.75米．
∵1.75＜3．
∴船的速度不变，它能安全通过此桥．

点评：本题考查了运用待定系数法求二次函数的解析式的运用，行程问题的数量关系的运用，有理数大小的比较的运用，解答时求出函数的解析式是关键．