题目内容
某果园有100棵橙子树,每一棵树平均结600个橙子,现准备多种一些橙子树以提高产量,据经验估计,每多种2棵树,平均每棵树就少结10个橙子.
(1)种多少棵橙子树,可以使果园橙子的总产量最多?最多为多少?
(2)增种多少棵橙子,可以使橙子的总产量在60400个以上?
(1)种多少棵橙子树,可以使果园橙子的总产量最多?最多为多少?
(2)增种多少棵橙子,可以使橙子的总产量在60400个以上?
考点:二次函数的应用
专题:
分析:(1)根据题意设多种x棵树,就可求出每棵树的产量,然后求出总产量y与x之间的关系式,配方后即可确定最值;
(2)根据函数关系式y=-5x2+100x+60000=60420,结合一元二次方程解法得出即可.
(2)根据函数关系式y=-5x2+100x+60000=60420,结合一元二次方程解法得出即可.
解答:解:(1)假设果园增种x棵橙子树,那么果园共有(x+100)棵橙子树,
∵每多种一棵树,平均每棵树就会少结5个橙子,
∴这时平均每棵树就会少结5x个橙子,
则平均每棵树结(600-5x)个橙子.
∵果园橙子的总产量为y,
∴则y=(x+100)(600-5x)
=-5x2+100x+60000=-5(x-10)2+60500,
故当增种橙树的棵数x取10棵时总产量最大,最大是60500个.
(3)当y=-5x2+100x+60000=60420时,
整理得出:x2-20x+84=0,
(x-14)(x-6)=0,
解得:x1=14,x2=6,
∵抛物线对称轴为直线x=10,
∴增种7到13棵橙子树时,可以使果园橙子的总产量在60420个以上.
通过以上计算可以发现,果园的树木棵数并不是越多越好,产量的多少取决于科学的计算果树的棵数.
∵每多种一棵树,平均每棵树就会少结5个橙子,
∴这时平均每棵树就会少结5x个橙子,
则平均每棵树结(600-5x)个橙子.
∵果园橙子的总产量为y,
∴则y=(x+100)(600-5x)
=-5x2+100x+60000=-5(x-10)2+60500,
故当增种橙树的棵数x取10棵时总产量最大,最大是60500个.
(3)当y=-5x2+100x+60000=60420时,
整理得出:x2-20x+84=0,
(x-14)(x-6)=0,
解得:x1=14,x2=6,
∵抛物线对称轴为直线x=10,
∴增种7到13棵橙子树时,可以使果园橙子的总产量在60420个以上.
通过以上计算可以发现,果园的树木棵数并不是越多越好,产量的多少取决于科学的计算果树的棵数.
点评:此题主要考查了二次函数的应用,准确分析题意,列出y与x之间的二次函数关系式是解题关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
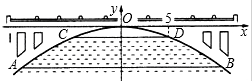 如图,有一抛物线型拱桥,在正常水位使水面宽AB=20m,当水位上升3m,水面宽CD=10m.
如图,有一抛物线型拱桥,在正常水位使水面宽AB=20m,当水位上升3m,水面宽CD=10m.
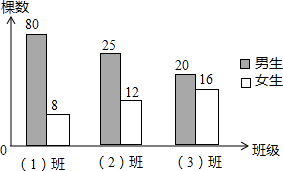 为了绿化环境,七年级(1)(2)(3)班参加植树造林活动,已知男同学4人每天植5棵树,女同学5人每天植4棵,如图统计图描述了三个班一天植树的棵树情况,则参加植树人数最多的班级是
为了绿化环境,七年级(1)(2)(3)班参加植树造林活动,已知男同学4人每天植5棵树,女同学5人每天植4棵,如图统计图描述了三个班一天植树的棵树情况,则参加植树人数最多的班级是