题目内容
当k为何值时,关于x的方程(k+1)x2+(2k+1)x+k-1=0有两个不相等的实数根?
考点:根的判别式,一元二次方程的定义
专题:计算题
分析:根据一元二次方程的定义和根的判别式的意义得到k+1≠0且△=(2k+1)2-4(k+1)(k-1)>0,然后解两个不等式求出它们的公共部分即可.
解答:解:根据题意得k+1≠0且△=(2k+1)2-4(k+1)(k-1)>0,
解得k>-
且k≠-1,
即当k>-
且k≠-1时,关于x的方程(k+1)x2+(2k+1)x+k-1=0有两个不相等的实数根.
解得k>-
| 5 |
| 4 |
即当k>-
| 5 |
| 4 |
点评:本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了一元二次方程的定义.

练习册系列答案
相关题目
 如图,若∠1=∠B,那么∠2与∠B有何数量关系?并说明理由;若∠4+∠C=180,那么∠3与∠C有何数量关系?并说明理由.
如图,若∠1=∠B,那么∠2与∠B有何数量关系?并说明理由;若∠4+∠C=180,那么∠3与∠C有何数量关系?并说明理由. 如图,在平面直角坐标系xOy中,抛物线y=
如图,在平面直角坐标系xOy中,抛物线y=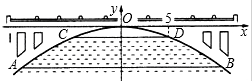 如图,有一抛物线型拱桥,在正常水位使水面宽AB=20m,当水位上升3m,水面宽CD=10m.
如图,有一抛物线型拱桥,在正常水位使水面宽AB=20m,当水位上升3m,水面宽CD=10m.