题目内容
2. 已知一次函数y=2x-3.
已知一次函数y=2x-3.(1)在给定的直角坐标系内作出它的图象;
(2)求它的图象与两坐标轴的交点坐标及两坐标轴所围成的三角形的面积.
分析 (1)首先根据函数解析式计算出与x、y轴的交点坐标,然后画图即可;
(2)根据与x、y轴的交点坐标,再利用三角形的面积公式计算即可.
解答  解:(1)如图:
解:(1)如图:
(2))∵当x=0时,y=-3,当y=0时,x=$\frac{3}{2}$,
∴一次函数y=2x-3的图象与x轴交于($\frac{3}{2}$,0),与y轴交与(0,-3),
∴S△AOB=$\frac{1}{2}×$$\frac{3}{2}$×3=$\frac{9}{4}$.
点评 此题主要考查了一次函数图象,以及一次函数图象上点的坐标特点,关键是掌握一次函数y=kx+b的图象与两坐标轴相交时的交点坐标:(0,b)(-$\frac{b}{k}$,0).

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG,$\widehat{AC}$,$\widehat{BC}$的中点分别是M,N,P,Q.若MP+NQ=12,AC+BC=16,则AB的长为( )
如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG,$\widehat{AC}$,$\widehat{BC}$的中点分别是M,N,P,Q.若MP+NQ=12,AC+BC=16,则AB的长为( )
 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG,$\widehat{AC}$,$\widehat{BC}$的中点分别是M,N,P,Q.若MP+NQ=12,AC+BC=16,则AB的长为( )
如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG,$\widehat{AC}$,$\widehat{BC}$的中点分别是M,N,P,Q.若MP+NQ=12,AC+BC=16,则AB的长为( )| A. | 9$\sqrt{2}$ | B. | $\frac{90}{7}$ | C. | 12 | D. | 16 |
10.下列代数式中符合书写要求的是( )
| A. | ab2×4 | B. | xy2÷3 | C. | $\frac{1}{4}xy$ | D. | $2\frac{1}{2}{a^2}b$ |
 如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. 如图,在△ABC中,AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
如图,在△ABC中,AB=AC,D是AC上的一点,CD=9,BC=15,BD=12. 如图,A、B两村和一条小河,要在河边L建一水厂Q向两村供水,若要使自来水厂到两村的输水管用料最省,厂址Q应选在哪个位置?请将上述情况下的自来水厂厂址标出,并保留作图痕迹.
如图,A、B两村和一条小河,要在河边L建一水厂Q向两村供水,若要使自来水厂到两村的输水管用料最省,厂址Q应选在哪个位置?请将上述情况下的自来水厂厂址标出,并保留作图痕迹.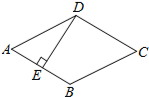 如图,菱形ABCD中,E是AB中点,DE⊥AB,则∠ADC的度数为120°.
如图,菱形ABCD中,E是AB中点,DE⊥AB,则∠ADC的度数为120°.