题目内容
3. 如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )
如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 ①利用全等三角形的判定得△ABE≌△ADF,再利用全等三角形的性质得出结论;
②利用等腰三角形的性质,三角形内角和定理,平行线的判定定理,同位角相等,两直线平行,得出结论;
③利用菱形的性质得AC⊥BD,得∠BCO=60°,再利用锐角三角函数求得EF;
④表示出三角形的面积,利用二次函数最值得出结论.
解答 解:∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动,
∴BE=DF,
在△ABE和△ADF中,
∵$\left\{\begin{array}{l}AB=AD\\∠B=∠D\\ BE=DF\end{array}\right.$,
∴△ABE≌△ADF(SAS),
∴AE=AF,
故①正确;
∴CE=CF,
∴∠CEF=$\frac{180°-∠C}{2}$,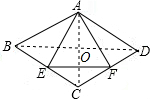
∵∠DBC=$\frac{180°-∠C}{2}$,
∴∠CEF=∠DBC,
∴EF∥BD,
故②正确;
当E、F分别为边BC、DC的中点时,
EF=$\frac{1}{2}$BD=BO,
连接AC,BD,
∵在菱形ABCD中,∠B=60°,
∴AC⊥BD,∠CBD=30°,
∴∠BCO=60°,
BO=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$•2BE=$\sqrt{3}$BE,
∴EF=$\sqrt{3}$BE,
故③正确;
∵△AEF的面积=菱形ABCD的面积-△ABE的面积-△ADF的面积-△CEF的面积
=$\frac{\sqrt{3}}{2}$AB2-$\frac{1}{2}$BE•AB×$\frac{\sqrt{3}}{2}$×2-$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×(AB-BE)2=-$\frac{\sqrt{3}}{4}$BE2+$\frac{\sqrt{3}}{4}$AB2,
∴△AEF的面积是BE的二次函数,
∴当BE=0时,△AEF的面积最大,
故④错误.
故正确的序号有①②③.
故选A.
点评 本题考查了菱形的性质、全等三角形的判定和等腰三角形的性质,熟练掌握菱形的性质和利用二次函数最值是解题关键.

 小题狂做系列答案
小题狂做系列答案| A. | a2•a3=a6 | B. | a2+a2=a4 | C. | a3÷a=a | D. | (-a2)3=-a6 |
| A. | 0 | B. | 18 | C. | 36 | D. | 72 |
| A. | $\frac{3}{8}$ | B. | $\frac{1}{8}$ | C. | -$\frac{1}{8}$ | D. | -$\frac{3}{8}$ |
 如图,已知AB是⊙O的切线,点A为切点,连接OB交⊙O于点C,∠B=38°,点D是⊙O上一点,连接CD,AD.则∠D等于( )
如图,已知AB是⊙O的切线,点A为切点,连接OB交⊙O于点C,∠B=38°,点D是⊙O上一点,连接CD,AD.则∠D等于( )| A. | 76° | B. | 38° | C. | 30° | D. | 26° |
 如图,直径AB、CD所夹锐角为60°,点P为$\widehat{BC}$上的一个动点(不与点B、C重合),PM、PN分别垂直于CD、AB,垂足分别为点M、N.若⊙O的半径为2cm,则在点P移动过程中,MN的长是否有变化否(填“是”或“否”),若有变化,写出MN的长度范围;若无变化,写出MN的长度:$\sqrt{3}$cm.
如图,直径AB、CD所夹锐角为60°,点P为$\widehat{BC}$上的一个动点(不与点B、C重合),PM、PN分别垂直于CD、AB,垂足分别为点M、N.若⊙O的半径为2cm,则在点P移动过程中,MN的长是否有变化否(填“是”或“否”),若有变化,写出MN的长度范围;若无变化,写出MN的长度:$\sqrt{3}$cm.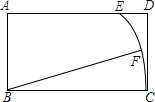 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为$\frac{1}{3}$.
如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为$\frac{1}{3}$. 如图,△ABC是等腰直角三角形,点O是斜边BC的中点,点E在AC上,点D在AB上,∠DOE=45°.若BD=9,CE=8,求DE的长.
如图,△ABC是等腰直角三角形,点O是斜边BC的中点,点E在AC上,点D在AB上,∠DOE=45°.若BD=9,CE=8,求DE的长.