题目内容
解方程:
(1)x2+2x=2;
(2)(x+3)(x-1)=5;
(3)(y-1)2+2y(y-1)=0;
(4)(2x+3)2=x2-8x+16.
(1)x2+2x=2;
(2)(x+3)(x-1)=5;
(3)(y-1)2+2y(y-1)=0;
(4)(2x+3)2=x2-8x+16.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:计算题
分析:(1)方程利用配方法求出解即可;
(2)方程整理后,利用因式分解法求出解即可;
(3)方程利用因式分解法求出解即可;
(4)方程整理后,利用平方根定义计算求出解即可.
(2)方程整理后,利用因式分解法求出解即可;
(3)方程利用因式分解法求出解即可;
(4)方程整理后,利用平方根定义计算求出解即可.
解答:解:(1)配方得:x2+2x+1=3,即(x+1)2=3,
开方得:x+1=±
,
解得:x1=-1+
,x2=-1-
;
(2)方程整理得:x2+2x-8=0,即(x-2)(x+4)=0,
可得x-2=0或x+4=0,
解得:x1=2,x2=-4;
(3)分解因式得:(y-1)(y-1+2y)=0,
可得y-1=0或3y-1=0,
解得:y1=1,y2=
;
(4)方程整理得:(2x+3)2=(x-4)2,
开方得:2x+3=x-4或2x+3=4-x,
解得:x1=-7,x2=
.
开方得:x+1=±
| 3 |
解得:x1=-1+
| 3 |
| 3 |
(2)方程整理得:x2+2x-8=0,即(x-2)(x+4)=0,
可得x-2=0或x+4=0,
解得:x1=2,x2=-4;
(3)分解因式得:(y-1)(y-1+2y)=0,
可得y-1=0或3y-1=0,
解得:y1=1,y2=
| 1 |
| 3 |
(4)方程整理得:(2x+3)2=(x-4)2,
开方得:2x+3=x-4或2x+3=4-x,
解得:x1=-7,x2=
| 1 |
| 3 |
点评:此题考查了解一元二次方程-因式分解法,配方法,以及直接开平方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知方程-x2+x+m=0有两个不相等的实根,则抛物线y=-x2+x+m的顶点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD=( )
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD=( )| A、60° | B、90° |
| C、45° | D、75° |
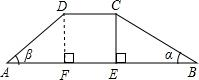 如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1,坝顶宽DC=2.5m,坝高5m.(整个大坝长5km,不改变坡角与坝底),需要多少土方?
如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1,坝顶宽DC=2.5m,坝高5m.(整个大坝长5km,不改变坡角与坝底),需要多少土方?