题目内容
19. 平行四边形ABCD中,CD=8,∠C=60°,点P为边BC上一动点,连接DP,作∠ADP的平分线交CB的延长线于F.
平行四边形ABCD中,CD=8,∠C=60°,点P为边BC上一动点,连接DP,作∠ADP的平分线交CB的延长线于F.(1)求证:PD=PF;
(2)若DP⊥CB,求DF的长.
分析 (1)由平行四边形的性质得出AD∥BC,得出∠ADF=∠F,再由角平分线定义证出∠F=∠PDF,即可得出PD=PF;
(2)由(1)得:PD=PF,由DP⊥CB,∠C=60°,得出△PDF是等腰直角三角形,∠PDC=30°,得出CP=$\frac{1}{2}$CD=4,由勾股定理求出PF=PD=$\sqrt{C{D}^{2}-C{P}^{2}}$=4$\sqrt{3}$,得出DF=$\sqrt{2}$PD=4$\sqrt{6}$即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠F,
∵DF平分∠ADP,
∴∠ADP=∠PDF,
∴∠F=∠PDF,
∴PD=PF;
(2)解:由(1)得:PD=PF,
∵DP⊥CB,∠C=60°,
∴△PDF是等腰直角三角形,∠PDC=90°-60°=30°,
∴CP=$\frac{1}{2}$CD=4,
∴PF=PD=$\sqrt{C{D}^{2}-C{P}^{2}}$=4$\sqrt{3}$,
∴DF=$\sqrt{2}$PD=4$\sqrt{6}$.
点评 本题考查了平行四边形的性质,等腰三角形的判定,勾股定理,等腰直角三角形的判定等知识;熟练掌握平行四边形的性质,由勾股定理求出PD是解决问题(2)的关键.

练习册系列答案
相关题目
14.正六边形具备而菱形不具备的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 每条对角线平分一组对边 |
8.下列说法不一定正确的是( )
| A. | 对顶角相等 | B. | 若同位角相等,则两直线平行 | ||
| C. | 若两直线平行,则内错角相等 | D. | 同旁内角互补 |
9.若三角形的三边长分别为$\sqrt{2}$,$\sqrt{6}$,2,则此三角形的面积为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
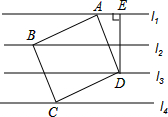 如图,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点A,B,C,D分别在l1,l2,l3,l4上,过点D作DE⊥l1于点E,已知相邻两条平行线之间的距离为1,求AE及正方形ABCD的边长.
如图,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点A,B,C,D分别在l1,l2,l3,l4上,过点D作DE⊥l1于点E,已知相邻两条平行线之间的距离为1,求AE及正方形ABCD的边长.
 如图,直线AB,CD交于点O,OE⊥AB,OD平分∠BOE,求∠AOC的度数.
如图,直线AB,CD交于点O,OE⊥AB,OD平分∠BOE,求∠AOC的度数.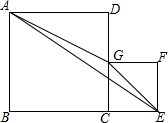 如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a、b.其中B、C、E在一条直线上,G在线段CD上.三角形AGE的面积为S.
如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a、b.其中B、C、E在一条直线上,G在线段CD上.三角形AGE的面积为S.