Question

18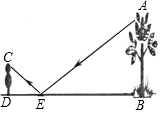．为了测量校园内水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把一面很小的镜子放在离树底（B）10米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A再用皮尺量得DE=2.0米，观察者目高CD=1.6米，则树（AB）的高度约为8米．

Answer 1

分析 根据镜面反射的性质求出△ABE∽△CDE，再根据其相似比解答．

解答 解：根据题意，易得∠CDE=∠ABE=90°，∠CED=∠AEB，
则△ABE∽△CDE，
则$\frac{BE}{DE}$=$\frac{AB}{CD}$，即$\frac{10}{2}$=$\frac{AB}{1.6}$，
解得：AB=8米．
故答案为：8．

点评 本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例是解答此题的关键．