题目内容
18.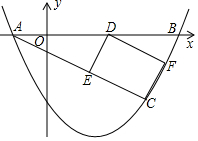 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c图象经过A(-1,0),B(4,0)两点.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c图象经过A(-1,0),B(4,0)两点.(1)求b,c的值;
(2)若C(m,1-m)是抛物线上位于第四象限内的点,D是线段AB上 的一个动点(不与A,B点重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连接EF,则线段EF的最小值为2.
分析 (1)因为抛物线与x轴交于(-1,0)(4,0),可以假设y=a(x+1)(x-4),由题意a=-$\frac{1}{2}$代入整理即可求出b、c.
(2)①利用待定系数法思想求出点C坐标,利用勾股定理的逆定理证明∠ACB=90°,由此即可解决问题.
②由四边形BECF是矩形,推出EF=CD,要求EF的最小值,即求CD的最小值,CD⊥AB时,CD最小,由此即可解决问题.
解答 (1)解:因为抛物线与x轴交于(-1,0)(4,0),可以假设y=a(x+1)(x-4)
∵a=$\frac{1}{2}$,
∴y=$\frac{1}{2}$(x+1)(x-4)=$\frac{1}{2}$x2-$\frac{3}{2}$x-2
∴b=-$\frac{3}{2}$,c=-2.
(2)①证明:把C(m,1-m)代入y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2得1-m=$\frac{1}{2}$m2-$\frac{3}{2}$m-2,
∴m1=-2 m2=3,
∵C在第四象限,
∴m=3,
∴c(3,-2),
∵BC∥DE DF∥AC,
∴四边形DECF是平行四边形,
∵AB2=25 AC2=20 BC2=5
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴四边形BECF是矩形.
②解:∵四边形BECF是矩形,
∴EF=CD,
要求EF的最小值,即求CD的最小值,
当CD⊥AB时,CD最小,
此时∵S△ABC=$\frac{1}{2}$•AC•BC=$\frac{1}{2}$•AB•CD,
∴CD=$\frac{AC•CB}{AB}$=$\frac{2\sqrt{5}•\sqrt{5}}{5}$=2.
故答案为2
点评 本题考查二次函数综合题、平行四边形的判定和性质、矩形的判定和性质、勾股定理的逆定理、垂线段最短等知识,解题的关键是灵活运用所学知识解决问题,学会利用垂线段最短解决最值问题,属于中考压轴题.

| A. | -3、-2 | B. | 3、-2 | C. | -3、2 | D. | 3、2 |
| A. | -6和-$\frac{1}{6}$ | B. | 6x2y和$\frac{2y{x}^{2}}{3}$ | C. | $\frac{1}{2}$a2b和-$\frac{1}{2}$ab2 | D. | 3m2n和-πm2n |
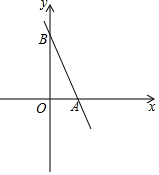 如图,直线y=-2x+3与x轴相交于点A,与y轴相交于点B.
如图,直线y=-2x+3与x轴相交于点A,与y轴相交于点B.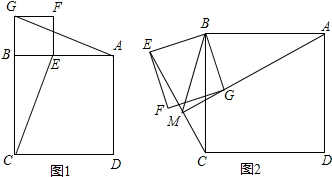
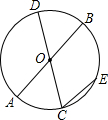 如图,AB、CD是⊙O的直径,弦CE∥AB,弧$\widehat{CE}$的度数为50°,求∠AOC的度数.
如图,AB、CD是⊙O的直径,弦CE∥AB,弧$\widehat{CE}$的度数为50°,求∠AOC的度数.