题目内容
一辆货车从货场A出发，向东行驶了2千米到达批发部B，继续向东行驶1.5千米到达商场C，又向西行驶了4.5千米到达超市D，最后回到货场．
（1）用1个单位长度表示1km，以向东为正方向，以货场为原点，画出数轴并在数轴上标明货场A，批发部B，商场C，超市D的位置．
（2）超市D在货场A什么方向、距离货场A多远？
（3）假设货车吗，每行驶1千米需耗油a升，则一共耗油多少升？
（1）用1个单位长度表示1km，以向东为正方向，以货场为原点，画出数轴并在数轴上标明货场A，批发部B，商场C，超市D的位置．
（2）超市D在货场A什么方向、距离货场A多远？
（3）假设货车吗，每行驶1千米需耗油a升，则一共耗油多少升？
考点：数轴,有理数的加减混合运算
专题：
分析：（1）根据数轴的特点分别画出各点即可；
（2）规定向东为正，根据相反意义的量分别表示“批发部B”、“商场C”、“超市D”后，列式计算；
（3）把这辆货车所走的路程（绝对值）相加，再与货车行驶1千米的耗油量相乘即可．
（2）规定向东为正，根据相反意义的量分别表示“批发部B”、“商场C”、“超市D”后，列式计算；
（3）把这辆货车所走的路程（绝对值）相加，再与货车行驶1千米的耗油量相乘即可．
解答：解：（1）如图所示：
（2）（+2）+（+1.5）+（-4.5）=-1．
所以超市D在货场A西1千米处．
（3）∵这辆货车一天所走的路程为2+1.5+4.5+1=9km，
∴本次这辆货车共耗油为9a升．
（2）（+2）+（+1.5）+（-4.5）=-1．
所以超市D在货场A西1千米处．
（3）∵这辆货车一天所走的路程为2+1.5+4.5+1=9km，
∴本次这辆货车共耗油为9a升．
点评：本题考查的是数轴的特点、应用具有相反意义的量列式计算及距离的定义，比较简单．
练习册系列答案
相关题目
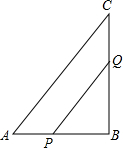如图，在△ABC中，∠B=90°，AB=6cm，BC=12cm，点P从点A开始，沿AB边向点B以每秒1cm的速度移动，点Q从点B开始，沿着BC边向点C以每秒2cm的速度移动，如果P、Q同时出发，问：经过几秒钟△PBQ的面积最大？最大面积是多少？
已知：如图，在△ABC中，AD是它的角平分线，且BD=CD，DE⊥AB，DF⊥AC，
如图，△ABC的中线BE、CF相交于点G，则GE：GB=（ ）| A、1：2 | B、1：3 |
| C、2：3 | D、2：5 |