题目内容
已知：如图，在△ABC中，AD是它的角平分线，且BD=CD，DE⊥AB，DF⊥AC，垂足分别是E，F．求证：EB=FC．
考点：全等三角形的判定与性质
专题：证明题
分析：易证DE=DF，即可证明RT△BDE≌RT△CDF，即可解题．
解答：证明：∵AD是∠BAC的角平分线，
∴DE=DF，
∵在RT△BDE和RT△CDF中，
，
∴RT△BDE≌RT△CDF，（HL）
∴EB=FC．
∴DE=DF，
∵在RT△BDE和RT△CDF中，
|
∴RT△BDE≌RT△CDF，（HL）
∴EB=FC．
点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证RT△BDE≌RT△CDF是解题的关键．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
相关题目
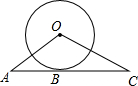如图，半径为3cm的⊙O与直线AC相切于点B，若AB=
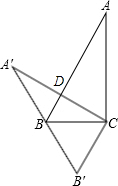在Rt△ABC中，∠ACB=90°，∠ABC=60°，将△ABC绕顶点C旋转到△A′B′C′的位置，使点B恰落在斜边A′B′上，设AC与AB相交于点D，则∠BDC=（ ）