��Ŀ����
��ͼ1��������y=ax2+bx-1����A��-1��0����B��2��0�����㣬��y���ڵ�C����PΪ�������ϵ�һ�����㣬����P��x��Ĵ��߽�ֱ��BC�ڵ�D����x���ڵ�E��
��1����ֱ��д�������߱���ʽ��ֱ��BC�ı���ʽ��
��2����ͼ1������P�ĺ�����Ϊ
ʱ����֤����OBD�ס�ABC��
��3����ͼ2������P�ڵ��������ڣ���OE=2PEʱ�����POD�������
��4�����Ե�O��C��DΪ������������ǵ���������ʱ����ֱ��д������P�����꣮

��1����ֱ��д�������߱���ʽ��ֱ��BC�ı���ʽ��
��2����ͼ1������P�ĺ�����Ϊ
| 2 |
| 3 |
��3����ͼ2������P�ڵ��������ڣ���OE=2PEʱ�����POD�������
��4�����Ե�O��C��DΪ������������ǵ���������ʱ����ֱ��д������P�����꣮

���㣺���κ����ۺ���,���������ε��ж�������
ר�⣺ѹ����,��������
��������1������ϵ����������ã�
��2���Ȱ�P��ĺ��������ֱ��y2=
x-1�����DE=
���Ӷ����DE=OE���ó���EOD=45�㣬��Ϊ��OAC=��EOD=45�㣬��OBD=��ABC��������á�OBD�ס�ABC��
��3���������������OD=CDʱ����
m2-m+1=
m2����OD=OCʱ����
m2-m+1=1����OC=CDʱ����
m2=1���ֱ���⣬������ã�
��2���Ȱ�P��ĺ��������ֱ��y2=
| 1 |
| 2 |
| 2 |
| 3 |
��3���������������OD=CDʱ����
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
����⣺��1����������y=ax2+bx-1��֪C��0��-1����
��y=ax2+bx-1����A��-1��0����B��2��0�����㣬
��
��
���
�������߱���ʽ��y1=
x2-
x-1��
��ֱ��BC�Ľ���ʽΪy=kx+b��
��
��
���
��
��ֱ��BC�ı���ʽ��y2=
x-1��
��2����ͼ1������P�ĺ�����Ϊ
ʱ����x=
����y2=
x-1��
��y2=
��
-1=-
��
��DE=
�֡�OE=
��
��DE=OE
�ߡ�OED=90��
���EOD=45��
�֡�OA=OC=1����AOC=90��
���OAC=45��
���OAC=��EOD
�֡ߡ�OBD=��ABC
��OBD�ס�ABC��
��3����ͼ2�����P������ΪP��x��
x2-
x-1��
��OE=x��PE=|
x2-
x-1|=-
x2+
x+1
�֡�OE=2PE
��x=2(-
x2+
x+1)
���x1=
��x2=-
������������ȥ����
��P��D��������ֱ�ΪP(
��-
)��D(
��
)��
��PD=
-(-
)=
-1
OE=
��S��POD=
•PD•OE=
•(
-1)•
=
��
��4��P1��1��-1����P2(
��-
)��P3(
��
)��P4(-
��
)��
��D��m��
m-1����
��OD2=m2+��
m-1��2=
m2-m+1��
OC2=1��CD2=m2+��-1-
m+1��2=
m2��
��OD=CDʱ����
m2-m+1=
m2�����m1=1��
��OD=OCʱ����
m2-m+1=1�����m2=
��
��OC=CDʱ����
m2=1�����m3=
��m4=-
��
��P1��1��-1����P2(
��-
)��P3(
��
)��P4(-
��
)��
��y=ax2+bx-1����A��-1��0����B��2��0�����㣬
��
|
���
|
�������߱���ʽ��y1=
| 1 |
| 2 |
| 1 |
| 2 |
��ֱ��BC�Ľ���ʽΪy=kx+b��
��
|
���
|
��ֱ��BC�ı���ʽ��y2=
| 1 |
| 2 |
��2����ͼ1������P�ĺ�����Ϊ
| 2 |
| 3 |
| 2 |
| 3 |
����y2=
| 1 |
| 2 |
��y2=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
��DE=
| 2 |
| 3 |
�֡�OE=
| 2 |
| 3 |
��DE=OE
�ߡ�OED=90��
���EOD=45��
�֡�OA=OC=1����AOC=90��
���OAC=45��
���OAC=��EOD
�֡ߡ�OBD=��ABC
��OBD�ס�ABC��
��3����ͼ2�����P������ΪP��x��
| 1 |
| 2 |
| 1 |
| 2 |
��OE=x��PE=|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�֡�OE=2PE
��x=2(-
| 1 |
| 2 |
| 1 |
| 2 |
���x1=
| 2 |
| 2 |
��P��D��������ֱ�ΪP(
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
��PD=
| ||
| 2 |
| ||
| 2 |
| 2 |
OE=
| 2 |
��S��POD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
2-
| ||
| 2 |
��4��P1��1��-1����P2(
| 4 |
| 5 |
| 27 |
| 25 |
2
| ||
| 5 |
-3-
| ||
| 5 |
2
| ||
| 5 |
-3+
| ||
| 5 |
��D��m��
| 1 |
| 2 |
��OD2=m2+��
| 1 |
| 2 |
| 5 |
| 4 |
OC2=1��CD2=m2+��-1-
| 1 |
| 2 |
| 5 |
| 4 |
��OD=CDʱ����
| 5 |
| 4 |
| 5 |
| 4 |
��OD=OCʱ����
| 5 |
| 4 |
| 4 |
| 5 |
��OC=CDʱ����
| 5 |
| 4 |
2
| ||
| 5 |
2
| ||
| 5 |
��P1��1��-1����P2(
| 4 |
| 5 |
| 27 |
| 25 |
2
| ||
| 5 |
-3-
| ||
| 5 |
2
| ||
| 5 |
-3+
| ||
| 5 |
���������⿼���˴���ϵ���������ʽ�����������Ƶ��ж��Լ��������۵�˼���Ӧ�ã�

��ϰ��ϵ�д�
�����Ŀ
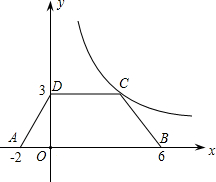 ��ͼ����������ABCD������ƽ������ϵ�У���֪A��-2��0����B��6��0����D��0��3����������������ͼ����C��
��ͼ����������ABCD������ƽ������ϵ�У���֪A��-2��0����B��6��0����D��0��3����������������ͼ����C��