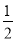题目内容
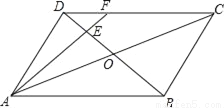
如图,在等边△ABC中,线段AM为BC边上的高,D是AM上的点,以CD为一边,在CD的下方作等边△CDE,连结BE.
(1)填空:∠ACB=____;∠CAM=____;
(2)求证:△AOC≌△BEC;
(3)延长BE交射线AM于点F,请把图形补充完整,并求∠BFM的度数;
(4)当动点D在射线AM上,且在BC下方时,设直线BE与直线AM的交点为F.∠BFM的大小是否发生变化?若不变,请在备用图中面出图形,井直接写出∠BFM的度数;若变化,请写出变化规律.
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目


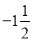 ,0.5.
,0.5.
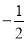 的相反数是( )
的相反数是( )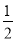 B. 2 C. -2 D. -
B. 2 C. -2 D. -