��Ŀ����
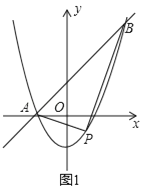
����Ŀ����ͼ1��������y��ax2+bx+c�Ķ��㣨0��5�����ҹ��㣨��3��![]() �������������ߵĽ���ʽ���ٽ���������⣺
�������������ߵĽ���ʽ���ٽ���������⣺
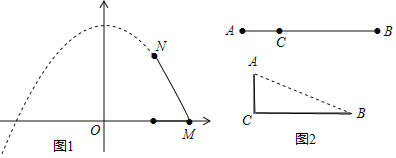
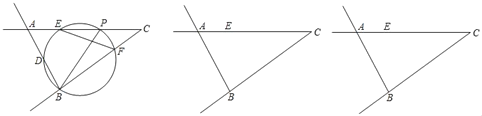
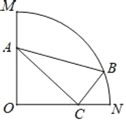
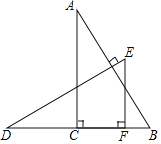
��Ӧ�ã�����1����ͼ2���߶�AB��d����ֵ�����������۳ɻ��ഹֱ������AC��CB����A��B����ľ���Ϊx����A��B��C�������ͼ�����ΪS����S��x�ĺ�����ϵ��ͼ��ʾ��������y��ax2+bx+c��MN֮��IJ��֣�M��x���ϣ���
��1����գ��߶�AB�ij���d���� �������ۺ�A��B����ľ���x��ȡֵ��Χ���� ������S��3�����Ƿ���ڵ�C����AB�ֳ����Σ����������������������� ���������S��1.5ʱ����C���߶�AB�ֳ����εij��ֱ����� ����
��2����գ�����ͼ1�У���ԭ��OΪԲ�ģ�A��B����ľ���xΪ�뾶�ġ�O��������C��AB��������AC��CB�ĺ���ͼ���߶Σ�����Բ��O���ú���ͼ��ľ���Ϊh����h���� �����ú���ͼ�����O��λ�ù�ϵ���� ����
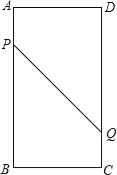
������������2��һ��ֱ��������б�߳�Ϊc����ֵ�����������ΪS���ܳ�Ϊx��֤��S��x�Ķ��κ�������ú�����ϵʽ������x��ȡֵ��Χ����ӦS��ȡֵ��Χ��
���𰸡������ߵĽ���ʽΪ��y����![]() x2+5����1��2
x2+5����1��2![]() 0��x��2
0��x��2![]() �����ܣ�
�����ܣ�![]() +
+![]() ��
��![]() ��
��![]() ����2��
����2��![]() ����������л��ཻ����3����ӦS��ȡֵ��ΧΪS��
����������л��ཻ����3����ӦS��ȡֵ��ΧΪS��![]() c2��
c2��
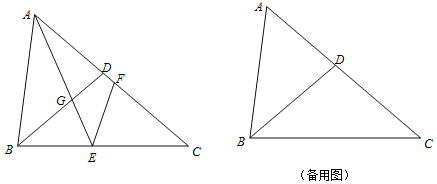
��������
�����㣨0��5�����㣨��3��![]() �����������ߵĶ���ʽ������������ʽ��
�����������ߵĶ���ʽ������������ʽ��
��1���������ߵĽ���ʽ�������M�����꣬�ɶ��κ�����ͼ�����ʼ����ж�d��ֵ������d��ֵ�жϳ�x��ȡֵ��Χ���ֱ�S��3��1��5���������߽���ʽ�����������C���߶�AB�ֳ����εij���
��2����AC��y��CB��x����ֱ��д����C��AB��������AC��CB�ĺ�������ʽ��������ͼ��֤��OPMΪ����ֱ�������Σ�����O��OH��PM�ڵ�H����OH��![]() PM��
PM��![]() ������������۳�AC��CB�ĺ���ͼ���߶�PM�����O��λ�ù�ϵ��
������������۳�AC��CB�ĺ���ͼ���߶�PM�����O��λ�ù�ϵ��
��3����ֱ�������ε���ֱ�DZ߳��ֱ�Ϊa��b���ɹ��ɶ�������ȫƽ��ʽ����֤��S��x�Ķ��κ���������д��x��ȡֵ��Χ����ӦS��ȡֵ��Χ��
�⣺��������y��ax2+bx+c�Ķ��㣨0��5����
��y��ax2+5��
���㣨��3��![]() �����룬
�����룬
��![]() ��a������3��2+5��
��a������3��2+5��
��a��![]() ��
��
�������ߵĽ���ʽΪ��y��![]() ��
��
��1����S��x�ĺ�����ϵ��ͼ��ʾ��������y��ax2+bx+c��MN֮��IJ��֣�M��x���ϣ���
��y��![]() ����y��0ʱ��x1��2
����y��0ʱ��x1��2![]() ��x2����2
��x2����2![]() ��
��
��M��2![]() ��0����
��0����
����x��2![]() ʱ��S��0��
ʱ��S��0��
��d��ֵΪ2![]() ��
��
�����ۺ�A��B����ľ���x��ȡֵ��Χ��0��x��2![]() ��
��
��S��3 ʱ����AC��a����BC��2![]() ��a��
��a��
��![]() a��2
a��2![]() ��a����3��
��a����3��
��������a2��2![]() a+6��0��
a+6��0��
�ߡ���b2��4ac����4��0��
�����ʵ������
��S��1.5ʱ����AC��a����BC��2![]() ��a��
��a��
��![]() a��2
a��2![]() ��a����1.5��
��a����1.5��
��������a2��2![]() a+3��0��
a+3��0��
���![]()
![]() ��
��
�൱a��![]() ʱ��2
ʱ��2![]() ��a��
��a��![]() ��
��
��a��![]() ʱ��2
ʱ��2![]() ��a��
��a��![]() ��
��
�������S��1.5ʱ����C���߶�AB�ֳ����εij��ֱ���![]() ��
��![]() ��
��
�ʴ�Ϊ��2![]() ��0��x��2
��0��x��2![]() �����ܣ�
�����ܣ�![]() ��
��![]() ��
��
��2����AC��y��CB��x��
��y����x+2![]() ����ͼ1��ʾ���߶�PM��
����ͼ1��ʾ���߶�PM��
��P��0��2![]() ����M��2
����M��2![]() ��0����
��0����
���OPMΪ����ֱ�������Σ�
��PM��![]() OP��2
OP��2![]() ��
��
����O��OH��PM�ڵ�H��
��OH��![]() PM��
PM��![]() ��
��
�൱0��x��![]() ʱ��AC��CB�ĺ���ͼ���߶�PM�����O���룻
ʱ��AC��CB�ĺ���ͼ���߶�PM�����O���룻
��x��![]() ʱ��AC��CB�ĺ���ͼ���߶�PM�����O���У�
ʱ��AC��CB�ĺ���ͼ���߶�PM�����O���У�
��![]() ��x��2
��x��2![]() ʱ��AC��CB�ĺ���ͼ���߶�PM�����O�ཻ��
ʱ��AC��CB�ĺ���ͼ���߶�PM�����O�ཻ��
�ʴ�Ϊ��![]() ����������л��ཻ��
����������л��ཻ��
��3����ֱ�������ε���ֱ�DZ߳��ֱ�Ϊa��b��
��![]() ��
��
�ߣ�a+b��2��a2+b2+2ab��
�ࣨx��c��2��c2+2ab��
��![]() ��
��
��S��![]() ��
��
��x��ȡֵ��ΧΪ��x��c��
����ӦS��ȡֵ��ΧΪS��![]() ��
��


 ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�