Question

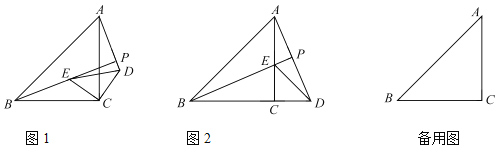
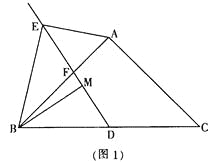
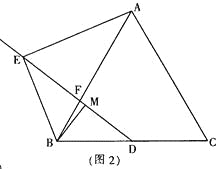
【题目】如图，已知△ABC中，AB＝8，BC＝10，AC＝12，D是AC边上一点，且AB2＝ADAC，连接BD，点E、F分别是BC、AC上两点（点E不与B、C重合），∠AEF＝∠C，AE与BD相交于点G．

（1）求BD的长；

（2）求证△BGE∽△CEF；

（3）连接FG，当△GEF是等腰三角形时，直接写出BE的所有可能的长度．

Answer 1

【答案】（1）；（2）见解析；（3）4或﹣5+或﹣3+

【解析】

（1）证明△ADB∽△ABC，可得，由此即可解决问题．

（2）想办法证明∠BEA=∠EFC，∠DBC=∠C即可解决问题．

（3）分三种情形构建方程组解决问题即可．

（1）∵AB=8，AC=12，又∵AB2=ADAC

∴

∵AB2=ADAC，

∴，

又∵∠BAC是公共角

∴△ADB∽△ABC，

∴

∴=

∴．

（2）∵AC=12，，

∴，

∴BD=CD，

∴∠DBC=∠C，

∵△ADB∽△ABC

∴∠ABD=∠C，

∴∠ABD=∠DBC，

∵∠BEF=∠C+∠EFC，

即∠BEA+∠AEF=∠C+∠EFC，

∵∠AEF=∠C，

∴∠BEA=∠EFC，又∵∠DBC=∠C，

∴△BEG∽△CFE．

（3）如图中，过点A作AH∥BC，交BD的延长线于点H，设BE=x，CF=y，

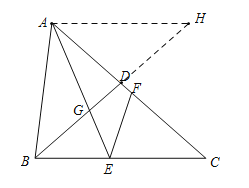
∵AH∥BC，

∴====，

∵BD=CD=，AH=8，

∴AD=DH=，

∴BH=12，

∵AH∥BC，

∴=，

∴=，

∴BG=，

∵∠BEF=∠C+∠EFC，

∴∠BEA+∠AEF=∠C+∠EFC，

∵∠AEF=∠C，

∴∠BEA=∠EFC，

又∵∠DBC=∠C，

∴△BEG∽△CFE，

∴=，

∴=，

∴y=；

当△GEF是等腰三角形时，存在以下三种情况：

①若GE=GF，如图中，则∠GEF=∠GFE=∠C=∠DBC，

∴△GEF∽△DBC，

∵BC=10，DB=DC=，

∴==，

又∵△BEG∽△CFE，

∴==，即=，

又∵y=，

∴x=BE=4；

②若EG=EF，如图中，则△BEG与△CFE全等，

∴BE=CF，即x=y，

又∵y=，

∴x=BE=﹣5+；

③若FG=FE，如图中，则同理可得==，

由△BEG∽△CFE，可得 ==，

即=，

又∵y=，

∴x=BE=﹣3+．