题目内容
16.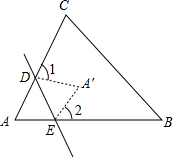 如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )
如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )| A. | α | B. | 2α | C. | 180°-α | D. | 180°-2α |
分析 根据三角形的内角和等于180°求出∠ADE+∠AED,再根据翻折变换的性质可得∠A′DE=∠ADE,∠A′ED=∠AED,然后利用平角等于180°列式计算即可得解.
解答 解:∵∠A=α,
∴∠ADE+∠AED=180°-α,
∵△ABC沿着DE折叠压平,A与A′重合,
∴∠A′DE=∠ADE,∠A′ED=∠AED,
∴∠1+∠2=180°-(∠A′ED+∠AED)+180°-(∠A′DE+∠ADE)=360°-2×(180°-α)=2α.
故选B.
点评 本题考查了三角形的内角和定理,翻折变换的性质,整体思想的利用求解更简便.

练习册系列答案
相关题目
6.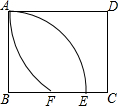 如图,矩形ABCD中,AB=12,BC=13,以B为圆心,BA为半径画弧,交BC于点E,以D为圆心,DA为半径画弧,交BC于点F,则EF的长为( )
如图,矩形ABCD中,AB=12,BC=13,以B为圆心,BA为半径画弧,交BC于点E,以D为圆心,DA为半径画弧,交BC于点F,则EF的长为( )
 如图,矩形ABCD中,AB=12,BC=13,以B为圆心,BA为半径画弧,交BC于点E,以D为圆心,DA为半径画弧,交BC于点F,则EF的长为( )
如图,矩形ABCD中,AB=12,BC=13,以B为圆心,BA为半径画弧,交BC于点E,以D为圆心,DA为半径画弧,交BC于点F,则EF的长为( )| A. | 3 | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
7.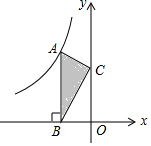 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( )
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( )
 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( )
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( )| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
4.化简$\frac{{m}^{2}}{m-n}$+$\frac{{n}^{2}}{n-m}$的结果是( )
| A. | n-m | B. | m-n | C. | m+n | D. | -m-n |
11.计算|-2017|的结果是( )
| A. | -2017 | B. | $-\frac{1}{2017}$ | C. | 2017 | D. | $\frac{1}{2017}$ |
1.不等式组$\left\{\begin{array}{l}{2x-1>1}\\{-x≤2}\end{array}\right.$的解集为( )
| A. | x>1 | B. | -2≤x<1 | C. | x≥-2 | D. | 无解 |
8.下列运算结果等于a6的是( )
| A. | a2•a3 | B. | a4+a2 | C. | a12÷a2 | D. | (a3)2 |
5. 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:
①a-b+c>0;
②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个互异实根.
其中正确结论的个数是( )
 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:①a-b+c>0;
②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个互异实根.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.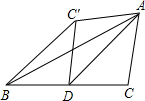 如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )
如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )
 如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )
如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 6 |