题目内容
17．已知x1，x2是方程x2-3x-1=0的两个实数根，那么下列结论正确的是（ ）| A． | x1+x2=-1 | B． | x1+x2=-3 | C． | x1+x2=1 | D． | x1+x2=3 |
分析 直接利用根与系数的关系求解．
解答 解：根据题意得，x1+x2=3，
故选D．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
7．
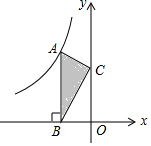如图，点A是反比例函数y=$\frac{k}{x}$的图象上的一点，过点A作AB⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC的面积为4，则k的值是（ ）
如图，点A是反比例函数y=$\frac{k}{x}$的图象上的一点，过点A作AB⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC的面积为4，则k的值是（ ）| A． | 4 | B． | -4 | C． | 8 | D． | -8 |
8．下列运算结果等于a6的是（ ）
| A． | a2•a3 | B． | a4+a2 | C． | a12÷a2 | D． | （a3）2 |
5．
如图是抛物线y=ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：
①a-b+c＞0；
②3a+b=0；
③b2=4a（c-n）；
④一元二次方程ax2+bx+c=n-1有两个互异实根．
其中正确结论的个数是（ ）
如图是抛物线y=ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：①a-b+c＞0；
②3a+b=0；
③b2=4a（c-n）；
④一元二次方程ax2+bx+c=n-1有两个互异实根．
其中正确结论的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
12．数轴上点A表示a，将点A沿数轴向左移动3个单位得到点B，设点B所表示的数为x，则x可以表示为（ ）
| A． | a-3 | B． | a+3 | C． | 3-a | D． | 3a+3 |
2．甲、乙两人同时从A地出发，骑自行车到B地，已知A、B两地的距离为50km，甲每小时比乙每小时多走2km，并且比乙先到20分钟，设乙每小时走xkm，则可列方程为（ ）
| A． | $\frac{50}{x}$-$\frac{50}{x-2}$=$\frac{1}{3}$ | B． | $\frac{50}{x}$-$\frac{50}{x+2}$=$\frac{1}{3}$ | C． | $\frac{50}{x+2}$-$\frac{50}{x}$=$\frac{1}{3}$ | D． | $\frac{50}{x-2}$-$\frac{50}{x}$=$\frac{1}{3}$ |
9．某市预计2022年初中毕业生学业考试10门学科整合后的满分值如下表：
请问根据130，120，100，150，120，40中，众数、中位数分别是（ ）
| 科目 | 语文 | 数学 | 英语 | 理化生 | 政史地 | 体育 |
| 满分值 | 130 | 120 | 100 | 120 | 120 | 40 |
| A． | 150，120 | B． | 120，120 | C． | 130，120 | D． | 120，100 |
6．
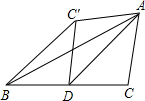如图，AD为△ABC的BC边上的中线，沿AD将△ACD折叠，C的对应点为C′，已知∠ADC=45°，BC=6，那么点B与C′的距离为（ ）
如图，AD为△ABC的BC边上的中线，沿AD将△ACD折叠，C的对应点为C′，已知∠ADC=45°，BC=6，那么点B与C′的距离为（ ）| A． | 3 | B． | 3$\sqrt{2}$ | C． | 3$\sqrt{3}$ | D． | 6 |