题目内容
10.解方程:(1)x2-25=0
(2)x2-6x=-9
(3)(x-1)2+2x(x-1)=0
(4)x2+x=12.
分析 (1)只需运用直接开平方法即可解决问题;
(2)只需运用配方法即可解决问题;
(3)只需运用因式分解法即可解决问题;
(4)只需运用因式分解法即可解决问题.
解答 解:(1)原方程可转化为
x2=25,
解得:x1=5,x2=-5;
(2)原方程可转化为
x2-6x+9=0,
配方得(x-3)2=0,
解得:x1=x2=3;
(3)原方程可转化为
(x-1)2-2x(x-1)=0,
即(x-1)(x-1-2x)=0,
也即(x-1)(-x-1)=0,
解得:x1=1,x2=-1;
(4)原方程可转化为
x2+x-12=0,
即(x+4)(x-3)=0,
解得:x1=-4,x2=3.
点评 本题主要考查的是运用适当的方法解一元二次方程,解一元二次方程通常有四种方法(直接开平方法、因式分解法、配方法、公式法),通常可根据一元二次方程的特点选择相应的方法.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
18.已知a+$\frac{1}{a}$=$\sqrt{5}$,则a-$\frac{1}{a}$=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | -$\sqrt{5}$ |
19. 如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
 如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
 如图所示是一个几何体从上面看到的图形,中间的数字表示该位置的小立方块的个数,请画出这个几何体从正面和左面看到的图形.
如图所示是一个几何体从上面看到的图形,中间的数字表示该位置的小立方块的个数,请画出这个几何体从正面和左面看到的图形.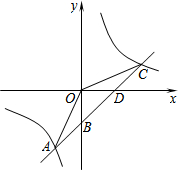 如图,一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.