题目内容
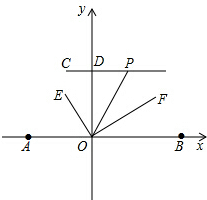 如图,过点C作CD⊥y轴于点D,点P为线段CD延长线上一动点,连接OP,OE平分∠AOP,OF⊥OE,当点P运动时,∠OPD:∠DOE的值是否会变化?若不会,求其值;若变化,请说明理由.
如图,过点C作CD⊥y轴于点D,点P为线段CD延长线上一动点,连接OP,OE平分∠AOP,OF⊥OE,当点P运动时,∠OPD:∠DOE的值是否会变化?若不会,求其值;若变化,请说明理由.考点:角的计算
专题:几何综合题
分析:利用平行线的性质,以及角平分线的定义表示出∠OPD和∠DOE即可求解.
解答:解:
的值不会变化,理由如下:
∵CD⊥y轴,AB⊥y轴,
∴∠CDO=∠DOB=90°,
∴AB∥CD,
∴∠OPD=∠POB,
∵OF⊥OE,
∴∠POF+∠POE=90°,∠BOF+∠AOE=90°,
∵OE平分∠AOP,
∴∠POE=∠AOE,
∴∠POF=∠BOF,
∴∠OPD=∠POB=2∠BOF,
∵∠DOE+∠DOF=∠BOF+∠DOF=90°,
∴∠DOE=∠BOF,
∴∠OPD=2∠BOF=2∠DOE,
∴
=2.
| ∠OPD |
| ∠DOE |
∵CD⊥y轴,AB⊥y轴,
∴∠CDO=∠DOB=90°,
∴AB∥CD,
∴∠OPD=∠POB,
∵OF⊥OE,
∴∠POF+∠POE=90°,∠BOF+∠AOE=90°,
∵OE平分∠AOP,
∴∠POE=∠AOE,
∴∠POF=∠BOF,
∴∠OPD=∠POB=2∠BOF,
∵∠DOE+∠DOF=∠BOF+∠DOF=90°,
∴∠DOE=∠BOF,
∴∠OPD=2∠BOF=2∠DOE,
∴
| ∠OPD |
| ∠DOE |
点评:该题目考查了角平分线的意义和平行线的性质,关键是紧扣题目中的条件和图形来进行推理.

练习册系列答案
相关题目
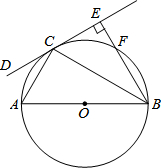 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,交圆与点F,连接AC、BC.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,交圆与点F,连接AC、BC. 如图,AB是圆O的直径,AD,BC,DC均为切线,求证:
如图,AB是圆O的直径,AD,BC,DC均为切线,求证: