题目内容
 如图,AB是圆O的直径,AD,BC,DC均为切线,求证:
如图,AB是圆O的直径,AD,BC,DC均为切线,求证:(1)DC=AD+BC;
(2)∠DOC=90°.
考点:切线的性质
专题:证明题
分析:(1)连接OE,由AD,BC,DC都为圆的切线,利用切线长定理得到DA=DE,CE=CB,由CD=DE+EC,等量代换即可得证;
(2)由DA=DE,OD为公共边,且夹角相等,利用SAS得到三角形AOD与三角形EOD全等,同理得到三角形EOC与三角形BOC全等,利用全等三角形的对应角相等得到两对角相等,再利用平角的定义及等式的性质即可得证.
(2)由DA=DE,OD为公共边,且夹角相等,利用SAS得到三角形AOD与三角形EOD全等,同理得到三角形EOC与三角形BOC全等,利用全等三角形的对应角相等得到两对角相等,再利用平角的定义及等式的性质即可得证.
解答: 证明:(1)连接OE,
证明:(1)连接OE,
∵AD,BC,DC均为圆O的切线,
∴DA=DE,BC=EC,
∴DC=DE+EC=AD+BC;
(2)连接OD,
∵AD,BC,DC均为圆O的切线,
∴DO、CO分别平分∠ADE、∠BCE,
∴∠ADO=∠EDO,∠ECO=∠BCO,
在△AOD和△EOD中,
,
∴△AOD≌△EOD(SAS),
同理△ECO≌△BCO,
∴∠AOD=∠EOD,∠EOC=∠BOC,
∵∠AOD+∠DOE+∠EOC+∠COB=180°,
∴∠DOE+∠EOC=90°,
则∠DOC=90°.
 证明:(1)连接OE,
证明:(1)连接OE,∵AD,BC,DC均为圆O的切线,
∴DA=DE,BC=EC,
∴DC=DE+EC=AD+BC;
(2)连接OD,
∵AD,BC,DC均为圆O的切线,
∴DO、CO分别平分∠ADE、∠BCE,
∴∠ADO=∠EDO,∠ECO=∠BCO,
在△AOD和△EOD中,
|
∴△AOD≌△EOD(SAS),
同理△ECO≌△BCO,
∴∠AOD=∠EOD,∠EOC=∠BOC,
∵∠AOD+∠DOE+∠EOC+∠COB=180°,
∴∠DOE+∠EOC=90°,
则∠DOC=90°.
点评:此题考查了切线的性质,切线长定理,全等三角形的判定与性质,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
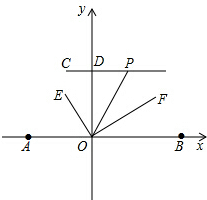 如图,过点C作CD⊥y轴于点D,点P为线段CD延长线上一动点,连接OP,OE平分∠AOP,OF⊥OE,当点P运动时,∠OPD:∠DOE的值是否会变化?若不会,求其值;若变化,请说明理由.
如图,过点C作CD⊥y轴于点D,点P为线段CD延长线上一动点,连接OP,OE平分∠AOP,OF⊥OE,当点P运动时,∠OPD:∠DOE的值是否会变化?若不会,求其值;若变化,请说明理由.