题目内容
13．如图，正三角形ABC（图1）和正五边形DEFGH（图2）的边长相同．点O为△ABC的中心，用5个相同的△BOC拼入正五边形DEFGH中，得到图3，则图3中的五角星的五个锐角均为（ ）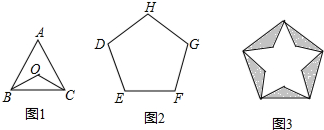
| A． | 36° | B． | 42° | C． | 45° | D． | 48° |
分析 根据图1先求出正三角形ABC内大钝角的度数是120°，则两锐角的和等于60°，正五边形的内角和是540°，求出每一个内角的度数，然后解答即可．
解答 解：如图，图1先求出正三角形ABC内大钝角的度数是180°-30°×2=120°，
180°-120°=60°，
60°÷2=30°，
正五边形的每一个内角=（5-2）•180°÷5=108°，
∴图3中的五角星的五个锐角均为：108°-60°=48°．
故选：D．
点评 本题主要考查了多边形的内角与外角的性质，仔细观察图形是解题的关键，难度中等．
练习册系列答案
相关题目
如图，在平行四边形ABCD中，∠C=66°，点E为AD上一点，AB=BE，求∠EBC的度数．
4．下列各整式中，次数为5次的单项式是（ ）
| A． | xy4 | B． | xy5 | C． | x+y4 | D． | x+y5 |
8．对一组数据：1，-2，4，2，5的描述正确的是（ ）
| A． | 中位数是4 | B． | 众数是2 | C． | 平均数是2 | D． | 方差是7 |
5．下列各式中正确的是（ ）
| A． | 3-2=-9 | B． | （72）3=75 | C． | x10÷x5=x2 | D． | $\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1 |
如图，△ABC中，∠BAC=60°，∠ABC=45°，AB=$\sqrt{2}$，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB、AC于E、F，连接EF，则线段EF长度的最小值为$\frac{\sqrt{3}}{2}$．