题目内容
18.先化简,再求值:$\frac{{x}^{2}-x}{x+1}$$•\frac{{x}^{2}-1}{{x}^{2}-2x+1}$-$\frac{x}{x+1}$,其中x2-2x-3=0的根.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{x(x-1)}{x+1}$•$\frac{x+1}{x-1}$-$\frac{x}{x+1}$
=x-$\frac{x}{x+1}$
=$\frac{{x}^{2}}{x+1}$,
解方程x2-2x-3=0得,x1=-1,x2=3,
∵当x=-1时,x+1=0,分式无意义,故舍去;
当x=3时,x+1≠0,
∴当x=3时,原式=$\frac{9}{3+1}$=$\frac{9}{4}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
6. 实数a在数轴上的位置如图所示,则下列说法正确的是( )
实数a在数轴上的位置如图所示,则下列说法正确的是( )
 实数a在数轴上的位置如图所示,则下列说法正确的是( )
实数a在数轴上的位置如图所示,则下列说法正确的是( )| A. | a的相反数是2 | B. | a的倒数等于2 | C. | a的绝对值是2 | D. | a的绝对值大于2 |
13.如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( )
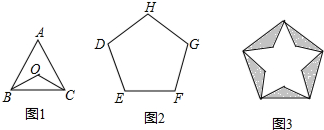

| A. | 36° | B. | 42° | C. | 45° | D. | 48° |
3.已知⊙O1和⊙O2的半径分别是3cm和5cm,圆心距O1O2是4cm,则这两个圆的位置关系是( )
| A. | 外离 | B. | 相交 | C. | 相切 | D. | 内含 |
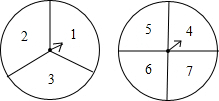 两个自由转动的转盘如图所示,一个分为3等份,分别标有数字1,2,3,另一个分为4等份,分别标有数字4,5,6,7.转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面A,B两种方案中选一种:方案A:猜“奇数”或猜“偶数”其中的一种;方案B:猜“是3的整数倍”或猜“不是3的整数倍”其中的一种.
两个自由转动的转盘如图所示,一个分为3等份,分别标有数字1,2,3,另一个分为4等份,分别标有数字4,5,6,7.转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面A,B两种方案中选一种:方案A:猜“奇数”或猜“偶数”其中的一种;方案B:猜“是3的整数倍”或猜“不是3的整数倍”其中的一种.