题目内容
1. 如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=$\sqrt{2}$,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为$\frac{\sqrt{3}}{2}$.
如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=$\sqrt{2}$,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为$\frac{\sqrt{3}}{2}$.
分析 由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径最短,如图,连接OE,OF,过O点作OH⊥EF,垂足为H,由Rt△ADB为等腰直角三角形,则AD=BD=1,即此时圆的直径为1,再根据圆周角定理可得到∠EOH=60°,则在Rt△EOH中,利用锐角三角函数可计算出EH=$\frac{\sqrt{3}}{4}$,然后根据垂径定理即可得到EF=2EH=$\frac{\sqrt{3}}{2}$.
解答 解:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径最短,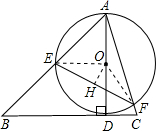
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
在Rt△ADB中,∠ABC=45°,AB=$\sqrt{2}$,
∴AD=BD=1,即此时圆的直径为1,
∵∠EOF=2∠BAC=120°,
而∠EOH=∠EOF,
∴∠EOH=60°,
在Rt△EOH中,EH=OE•sin∠EOH=$\frac{1}{2}$•sin60°=$\frac{\sqrt{3}}{4}$,
∵OH⊥EF,
∴EH=FH,
∴EF=2EH=$\frac{\sqrt{3}}{2}$,
即线段EF长度的最小值为$\frac{\sqrt{3}}{2}$.
故答案为$\frac{{\sqrt{3}}}{2}$.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了垂线段最短和解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( )
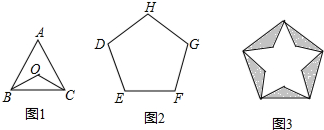

| A. | 36° | B. | 42° | C. | 45° | D. | 48° |
11.在下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 直角三角形 | B. | 正五边形 | C. | 菱形 | D. | 平行四边形 |
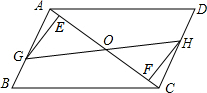 已知:如图,在?ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
已知:如图,在?ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O. 已知y是x的反比例函数,且当x=2时,y=-3,
已知y是x的反比例函数,且当x=2时,y=-3,