题目内容
 如图,在等腰梯形ABCD中,AD∥BC,AB=CD=AD=2cm,∠BAD=120°,P为AD的中点,在直线AD下方作∠BPE=120°,使边PE与等腰梯形的某一边所在直线相交于点E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD=AD=2cm,∠BAD=120°,P为AD的中点,在直线AD下方作∠BPE=120°,使边PE与等腰梯形的某一边所在直线相交于点E.(1)画出所有符合题意的示意图,并说明以点B、P、E为顶点的三角形是否与△ABP相似?
(2)求△BPA的面积.
考点:等腰梯形的性质,相似三角形的判定与性质
专题:
分析:(1)分点E在CD上时,根据等腰梯形同一底上的两个角相等可得∠D=∠BAD=120°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ABP=∠DPE,然后根据两组角对应相等的两个三角形相似求出△ABP和△DPE相似,根据相似三角形对应边成比例求出
=
=2,再根据两边对应成比例夹角相等两三角形相似求解即可;点E在直线BC上时,根据两直线平行,内错角相等可得∠APB=∠PBE,然后利用两组角对应相等两三角形相似证明;
(2)求出∠ABC=60°,然后求出等腰梯形的高,再根据三角形的面积公式列式计算即可得解.
| BP |
| PE |
| AB |
| PD |
(2)求出∠ABC=60°,然后求出等腰梯形的高,再根据三角形的面积公式列式计算即可得解.
解答:解:(1)如图1,点E在CD上时,
∵P为AD的中点,AB=AD,
∴AB=2AP=2PD,
∵等腰梯形ABCD中,∠BAD=120°,
∴∠D=∠BAD=120°,
∵∠BPE=120°,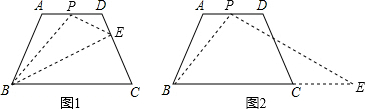
∴∠ABP+∠BAD=∠BPE+∠DPE,
∴∠ABP=∠DPE,
∴△ABP∽△DPE,
∴
=
=2,
又∵∠BAD=∠BPE=120°,
∴△ABP∽△PBE;
如图2,点E在直线BC上时,
∵AD∥BC,
∴∠APB=∠PBE,
又∵∠BAD=∠BPE=120°,
∴△ABP∽△PBE;
(2)∵AD∥BC,∠BAD=120°,
∴∠ABC=60°,
∴梯形的高=AB•
=2×
=
cm,
∵AD=2,点P是AD的中点,
∴AP=
×2=1,
∴△BPA的面积=
×1×
=
cm2.
∵P为AD的中点,AB=AD,
∴AB=2AP=2PD,
∵等腰梯形ABCD中,∠BAD=120°,
∴∠D=∠BAD=120°,
∵∠BPE=120°,
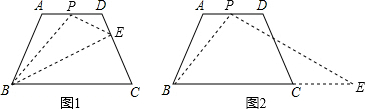
∴∠ABP+∠BAD=∠BPE+∠DPE,
∴∠ABP=∠DPE,
∴△ABP∽△DPE,
∴
| BP |
| PE |
| AB |
| PD |
又∵∠BAD=∠BPE=120°,
∴△ABP∽△PBE;
如图2,点E在直线BC上时,
∵AD∥BC,
∴∠APB=∠PBE,
又∵∠BAD=∠BPE=120°,
∴△ABP∽△PBE;
(2)∵AD∥BC,∠BAD=120°,
∴∠ABC=60°,
∴梯形的高=AB•
| ||
| 2 |
| ||
| 2 |
| 3 |
∵AD=2,点P是AD的中点,
∴AP=
| 1 |
| 2 |
∴△BPA的面积=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
点评:本题考查了等腰梯形,相似三角形的判定与性质,三角形的面积,难点在于(1)先利用相似三角形求出对应边成比例,然后再判断出另两个三角形相似.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,P是Rt△ABC的斜边BC上异于B、C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有
如图,P是Rt△ABC的斜边BC上异于B、C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有 如图,已知⊙I内切于△ABC,切点分别分别为D、E、F,试说明,∠BIC=90°+
如图,已知⊙I内切于△ABC,切点分别分别为D、E、F,试说明,∠BIC=90°+ 如图,在△ABC中,CF:EF:BE=3:2:1,BD:AD=2:3.求CH:HG:DG的比.
如图,在△ABC中,CF:EF:BE=3:2:1,BD:AD=2:3.求CH:HG:DG的比.